संख्यांच्या दुनियेत
संख्यांच्या दुनियेत
बालमोहन लिमये
(‘गणिताच्या निमित्ताने' ही १२ भागांची लेखमाला दोन आठवड्यांपूर्वी संपली. बालमोहन लिमये यांचे त्याच धर्तीवरील आणखी काही लिखाण क्रमशः प्रकाशित करत आहोत.)
आय. आय. टी.च्या परिसरात राहत असताना मी दररोज सकाळी लवकर उठून फिरायला जात असे. बरोबर एक-दोन प्राध्यापक मित्र पण असत. एकट्यानेच जायचे असले तर कधी कधी कंटाळा करता येतो, पण कुणी आपली वाट बघत असेल हे लक्षात आल्यावर चटकन बाहेर पडावे लागते. फिरता फिरता आम्ही अनेक बाबींवर गप्पा मारत असू, खास करून एकमेकांच्या विषयातल्या. एका रविवारी पदार्थविज्ञान विभागात काम करणारे माझे मित्र अनंत महाजन यांनी वेगवेगळ्या प्रकारच्या संख्यांचा विषय काढला. त्यांच्याकडे मेरी बोॲस (Mary Boas) हिने १९८३ साली लिहिलेले Mathematical Methods in Physical Sciences या नावाचे एक पुस्तक होते. त्यात संमिश्र संख्यांची महती गायिली होती, आणि पदार्थविज्ञान, विद्युत अभियांत्रिकी (Electrical Engineering) अशा अनेक विषयांच्या काही भागात या संख्यांवाचून पान हलणार नाही असे म्हटले होते. नेहमीच्या संख्यांशिवाय i ही आणखी एक संख्या मानायची व तिचा वर्ग -1 आहे असे समजले की नेहमीचेच नियम वापरून काम कसे भागते हे दाखवून दिले होते. पण माझ्या मित्राला हा अनोखा दिसणारा आणि विचित्र वागणारा i कुठून आला याचे कोडे पडले होते. आमचे रविवार सकाळचे फिरणे संपवून घरी परतल्यावर मी काही मूलभूत गोष्टी लिहून काढल्या आणि माझ्या मित्राला वाचायला दिल्या. नंतर आमच्या चर्चेतून निष्पन्न झालेली कहाणी आता सांगतो. संख्येच्या दुनियेत कुठून सुरुवात करून आपण कुठे पोचू शकतो, आणि त्याच्याही पलीकडे जाणे आवश्यक असते का, व शक्य असते का याचा विचार करू या. ही प्रक्रिया काही ठिकाणी कठीण वाटली तरी थोडीशी सबुरी बाळगली तर गणितातील काही पायाभूत गोष्टींचा परिचय करून घेता येईल.
परिमेय संख्या
1, 2, 3, 4, 5, 6, … इत्यादींपैकी कुठल्याही आकड्याला नैसर्गिक संख्या (natural number) किंवा धन पूर्णांक (positive integer) असे म्हणतात. एखादी नैसर्गिक संख्या 1 पेक्षा मोठी असेल व तिला दुसऱ्या कुठल्याच संख्येने भाग जात नसेल, तर तिला मूळ संख्या (prime number) असे म्हणतात. उदाहरणार्थ, 2, 3, 5 या मूळ संख्या आहेत, पण 4, 6 या मूळ संख्या नाहीत. नैसर्गिक संख्यांप्रमाणे मूळ संख्याही अनंत आहेत हे आपण सोप्या रीतीने सिद्ध करू शकतो. (पहा: गणिताच्या निमित्ताने, भाग ७) नैसर्गिक संख्यांशिवाय प्राचीन भारतीयांच्या विचारधारेतील रितेपणाच्या संकल्पनेचे मूर्त स्वरूप म्हणजे शून्य (zero) ही संख्या होय. ती 0 या चिह्नाने दाखवतात. आता t + 1 = 0 यासारखी समीकरणे सोडवण्यासाठी –1, –2, –3, ... इत्यादी ऋण पूर्णांक (negative integers) यांचा समावेश केला की आपल्याला सगळे पूर्णांक (integers) मिळतात. याच्या पुढे जाऊन 2t – 1 = 0 किंवा 2t + 1 = 0 यासारखी समीकरणे सोडवण्यासाठी अपूर्णांक (fractions) जरूर असतात; एका पूर्णांकाला दुसऱ्या पूर्णांकाने (0 खेरीज) भागले की आपल्याला सगळे अपूर्णांक (fractions) मिळतात. उदाहरणार्थ, 1/2, 3/2, 2/3, –1/2, –5/3 हे अपूर्णांक आहेत. आतापर्यंत वर्णन केलेल्या प्रत्येक संख्येला परिमेय संख्या (rational number) असे म्हणतात. दोन परिमेय संख्यांची बेरीज किंवा वजाबाकी केली तर, तसेच त्यांचा गुणाकार किंवा भागाकार केला तर आपल्याला परिमेय संख्याच मिळतात. सर्व परिमेय संख्या आपण एका आडव्या सरळ रेषेवरील काही बिंदूंनी दाखवू शकतो.
अपरिमेय संख्या
आता t2 – 2 = 0 हे समीकरणाचा विचार करू या. सरळ रेषेवरील एका विशिष्ट बिंदूच्या साह्याने हे समीकरण सोडवता येते हे दाखवण्यासाठी आपण शाळेत शिकलेल्या भूमितीचा उपयोग करू या. काटकोन त्रिकोणातील काटकोनाशेजारच्या दोन्ही बाजूंची लांबी दिली असेल, तर त्या त्रिकोणाच्या कर्णाची लांबी किती असते याचे उत्तर पायथॅगोरसचा सिद्धांत वापरून देता येते. या सिद्धांतानुसार, काटकोन त्रिकोणातील कर्णाची लांबी x असेल व इतर दोन बाजूंची लांबी y आणि z असेल, तर x2 = y2 + z2 असे समीकरण बनते. उदाहरणार्थ, y = 3 असेल आणि z = 4 असेल, तर x2 = 32 + 42 = 25, व म्हणून या कर्णाची लांबी x = 5.
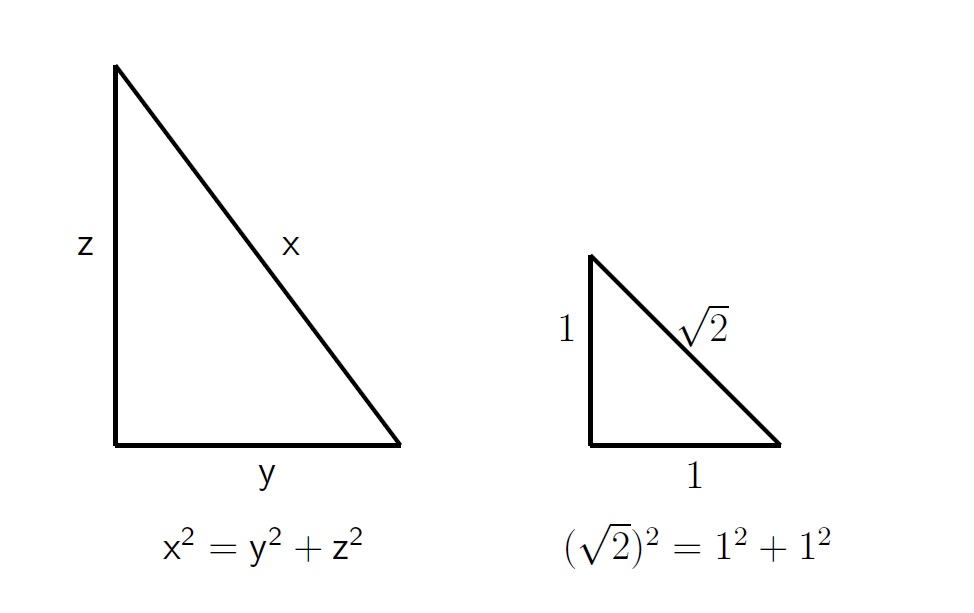
आता समजा आपल्या काटकोन त्रिकोणात y = 1 आहे आणि z = 1 आहे, व म्हणून x2 = 12 + 12 = 2, म्हणजे या कर्णाच्या लांबीचा वर्ग 2 असला पाहिजे. या कर्णाचे एक टोक सरळ रेषेवरील 0 या बिंदूवर ठेवले व तो रेषेवर उजवीकडे लावून ठेवला, तर त्याचे दुसरे टोक ज्या बिंदूवर असेल तो बिंदू या कर्णाची लांबी दाखवतो. लांबीचा वर्ग 2 असल्याने तो बिंदू t2 – 2 = 0 हे समीकरण सोडवतो. त्या बिंदूसाठी √2 हे चिह्न वापरतात आणि तो बिंदू 2 या संख्येचे वर्गमूळ (square root) आहे असे म्हणतात. हा बिंदू 1 या बिंदूच्या उजवीकडे आणि 2 या बिंदूच्या डावीकडे असणार, कारण 12 = 1 < (√2)2 = 2 < 22 = 4.
मात्र √2 या बिंदूने कोणतीही परिमेय संख्या दाखवली जात नाही. ही गोष्ट पायथागोरसच्या काळापासून म्हणजे इसवी सनापूर्वीच्या सहाव्या शतकापासून लोकांना माहित होती. ती सिद्ध करण्यासाठी क्षणभर असे गृहित धरू की p आणि q या नैसर्गिक संख्या अशा आहेत की (p/q)2 – 2 = 0, म्हणजे p2 = 2q2. आता p या संख्येचा 2 हा मूळ अवयव (prime factor) जितक्या वेळा असतो, त्याच्या दुप्पट वेळा p2 या संख्येचा तो मूळ अवयव असतो. उदाहरणार्थ, 2 हा 4 चा दोनदा, 6 चा एकदा, तर 8 चा तीनदा मूळ अवयव आहे, पण तो 42 = 16 चा चारदा, 62 = 36 चा दोनदा, तर 82 = 64 चा सहा वेळा मूळ अवयव आहे. अशाप्रकारे आपल्याला दिसून येते की p2 या संख्येचा 2 हा मूळ अवयव सम वेळा असतो. तसेच q2 या संख्येचा 2 हा मूळ अवयव सम वेळा असतो, व म्हणून 2q2 या संख्येचा तो विषम वेळा मूळ अवयव असतो. पण p2 = 2q2, म्हणजे p2 आणि 2q2 ही एकच संख्या आहे; तिचा 2 हा मूळ अवयव सम वेळा तरी असेल किंवा विषम वेळा तरी असेल, दोन्ही नाही. ही विसंगती निर्माण होण्याचे कारण असे की आपण गृहित धरलेले समीकरण (p/q)2 – 2 = 0 चुकीचे आहे, म्हणजेच 2 ही संख्या परिमेय संख्येचा वर्ग असू शकत नाही, किंवा √2 ही परिमेय संख्या नाही. अशा प्रकारच्या सिद्धतेला विरोधजन्य सिद्धता (proof by contradiction) असे म्हणतात.
आडव्या सरळ रेषेवर परिमेय संख्या सोडून उरलेले जे बिंदू आहेत, त्या बिंदूंना अपरिमेय संख्या (irrational numbers) असे म्हणतात. परिमेय संख्यांप्रमाणेच अपरिमेय संख्याही अनंत आहेत. वस्तुतः अपरिमेय संख्या परिमेय संख्यांपेक्षा एका अर्थाने जास्तच आहेत, पण नेमक्या कोणत्या अर्थाने याकडे आत्ता वळायला नको.
वास्तव संख्या
सरळ रेषेवरील बिंदू (points on the line) ज्या संख्या दर्शवतात, त्यांना वास्तव संख्या (real number) असे म्हणतात, आणि म्हणून आडव्या सरळ रेषेला संख्यारेषा असे नाव देतात. परिमेय संख्या आणि अपरिमेय संख्या मिळून वास्तव संख्या बनतात.
1, 2, 3, 0, –1, –2, –3, 3/2, 2/3, –1/2, –5/3, √2 ही सर्व वास्तव संख्यांची उदाहरणे आहेत.
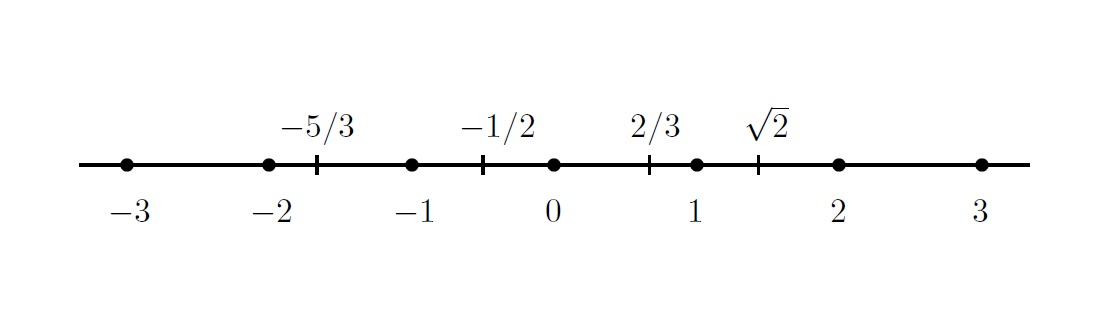
संख्यारेषा
वास्तव संख्यांची बेरीज व वजाबाकी, आणि त्यांचा गुणाकार व भागाकार आपण नेहमीचे नियम वापरून करत आलो आहोत. त्या शिवाय, जर r ही एक धन वास्तव संख्या (positive real number) असेल, तर x अशी एक आणि एकच धन वास्तव संख्या असते की जिचा वर्ग r आहे, म्हणजे x2 = r. या वास्तव संख्येला r या संख्येचे वर्गमूळ म्हणतात, व ते √r किंवा r½ या चिह्नाने दाखवतात. आता समजा r ही 3, 5, 7, ... या सारखी एक मूळ संख्या आहे. आपण 2 ही संख्या कोणत्याही परिमेय संख्येचा वर्ग असू शकत नाही हे जसे सिद्ध केले, अगदी अशीच सिद्धता देऊन आपण म्हणू शकतो की 3, 5, 7 यासारखी कोणतीही मूळ संख्या परिमेय संख्येचा वर्ग असू शकत नाही. म्हणून √3, √5, √7 या सारखे कोणत्याही मूळ संख्येचे वर्गमूळ ही एक अपरिमेय संख्या असते.
बऱ्याच जणांना माहीत असलेल्या e आणि π (पाय) ह्या सुध्दा अपरिमेय संख्या आहेत, पण हे सिद्ध करणे मात्र तितके सोपे नाही.
बैजिक संख्या
समजा x ही एक वास्तव संख्या आहे. जर n ह्या नैसर्गिक संख्येसाठी आणि a0, a1, ... an ह्या पूर्णांकांसाठी a0 + a1x + ... + an xn = 0 असे समीकरण साध्य होत असेल, तर x ही बैजिक (algebraic) संख्या आहे असे म्हणतात. सर्व परिमेय संख्या बैजिक असतात, कारण जर p हा एक पूर्णांक, q ही एक नैसर्गिक संख्या आणि x = p/q असेल, तर qx – p = 0 हे समीकरण साध्य होते. काही अपरिमेय संख्या बैजिक असू शकतात. उदाहरणार्थ, x = √2 असेल तर x2 - 2 = 0 हे समीकरण साध्य होते, त्याचप्रमाणे p ही मूळ संख्या असेल,तर x = √p ही संख्या अपरिमेय आहे, पण x2 - p = 0 हे समीकरण साध्य होत असल्याने x ही बैजिक संख्या आहे. मात्र बऱ्याचशा अपरिमेय संख्या बैजिक नसतात. उदाहरणार्थ, e आणि π या संख्या बैजिक नाहीत, पण ते सिद्ध करणे खूपच कठीण आहे. जर एखादी वास्तव संख्या बैजिक नसेल तर ती अबैजिक (transcendental) संख्या आहे असे म्हणतात.
संमिश्र संख्या
कुठल्याही वास्तव संख्येचा वर्ग केला, तर मिळणारी संख्या कधीच ऋण नसते. त्यामुळे t2 + 1 = 0 , म्हणजे t2 = –1, हे समीकरण सोडवण्यासाठी वास्तव संख्या पुरेशा नाहीत. याचा अर्थ असा की आपल्या आडव्या सरळ रेषेवरील कुठलाही बिंदू हे काम बजावू शकत नाही. या कारणामुळे आपल्याला या आडव्या सरळ रेषेवरील बिंदूंच्या पलीकडे जाणे भाग पडते. आडव्या सरळ रेषेवरील 0 या बिंदूतून जाणारी व तिला काटकोनात छेदणारी उभी सरळ रेषा काढली, तर या दोन रेषा एक प्रतल (plane) बनवतात. या प्रतलावरील बिंदूला (point on the plane) संमिश्र संख्या (complex number) असे म्हणतात. आता z ही एक संमिश्र संख्या असेल, तर ती x आणि y या दोन वास्तव संख्यांच्या साह्याने z = (x, y) अशी दर्शविता येते; यातील x ही वास्तव संख्या z या संमिश्र संख्येचा पहिला निर्देशक (first coordinate) आहे, आणि y ही वास्तव संख्या तिचा दुसरा निर्देशक (second coordinate) आहे असे म्हणायचे. आडव्या सरळ रेषेवरील x हा कुठलाही बिंदू आता प्रतलावरील (x, 0) या बिंदूने दाखवता येतो, व म्हणून सगळ्या वास्तव संख्या संमिश्र संख्यांचा एक भाग बनतात. काटकोनात काढलेल्या उभ्या सरळ रेषेवरील (0, y) अशा बिंदूला कल्पित संख्या (imaginary number) असे म्हणतात. खरे म्हणजे असे म्हणण्यात कोणताच कल्पनाविलास नाही, पण एके काळी सरळ रेषेबाहेरील कशालाही संख्या म्हणायला कोणी धजत नसे, व म्हणून ‘कल्पित संख्या’ असे नाव पडले. वास्तव संख्यांप्रमाणे कल्पित संख्यादेखील संमिश्र संख्यांत समाविष्ट आहेत. परंतु संमिश्र संख्यांचा संच यापेक्षा खूपच मोठा आहे. उदाहरणार्थ, (3, 2) ही वास्तव संख्या नाही व कल्पित संख्याही नाही, पण ती एक संमिश्र संख्या आहे. (0, 0) हा बिंदू आडव्या व उभ्या अशा दोन्ही रेषांवर आहे, व म्हणून (0, 0) ही वास्तव संख्या आहे व ती कल्पित संख्याही आहे असे मानायचे.
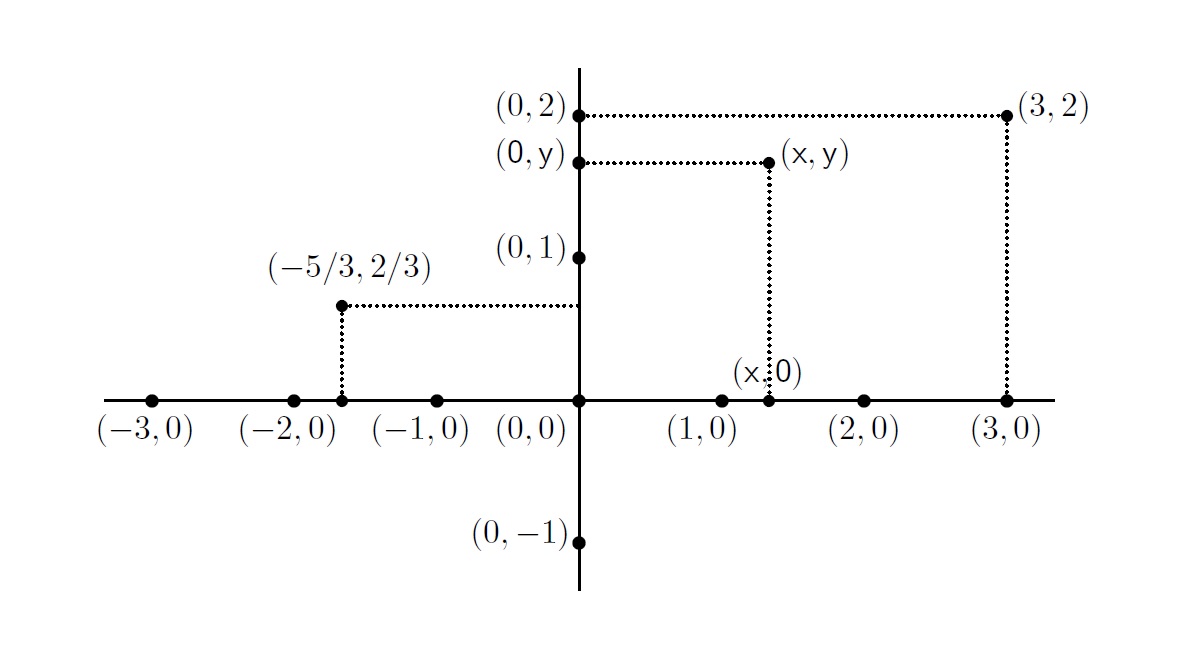
संमिश्र संख्या
वरील आकृतीत अनेक संमिश्र संख्या दाखवल्या आहेत. त्यापैकी आडव्या रेषेवरील सगळ्या संख्या वास्तव संख्या आहेत, तर उभ्या रेषेवरील सगळ्या संख्या कल्पित संख्या आहेत.
संमिश्र संख्यांची बेरीज-वजाबाकी
समजा z = (x, y) आणि w = (u, v) या संमिश्र संख्या आहेत. त्यांची बेरीज
अशी करायची. उदाहरणार्थ, (2, 3) + (3, 1) = (2 + 3, 3 + 1) = (5, 4). तसेच z + z = (x + x, y + y), म्हणजेच 2z = (2x, 2y) अशी z या संमिश्र संख्येची दुप्पट होते. आपल्याला सहज दिसून येते की z = (x, y) ही कुठलीही संमिश्र संख्या असेल तर ती (x, 0) या वास्तव संख्येची आणि (0, y) या कल्पित संख्येची बेरीज करून मिळते.
बेरजेच्या व्याख्येचा भूमितीच्या दृष्टीने असा अर्थ लावता येतो: z = (x, y) व (0, 0) या दोन बिंदूंना जोडणारी, तसेच w = (u, v) व (0, 0) या दोन बिंदूंना जोडणारी अशा रेषा काढायच्या. या दोन रेषा ज्याच्या लगतच्या बाजू आहेत असा समांतरभुज चौकोन काढला, तर त्याचा चौथा शिरोबिंदू असतो (x + u, y + v), व म्हणून तो z आणि w यांची बेरीज दर्शवितो.
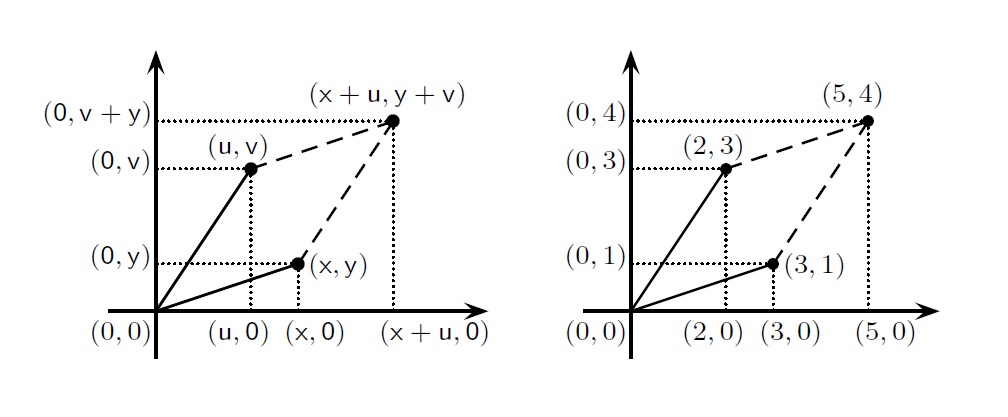
बेरीज करता आली, तशी वजाबाकीही करता आली पाहिजे. आता z = (x, y) या संमिश्र संख्येसाठी आपण –z = (–x, –y) अशी व्याख्या करू या. मग आपल्याला
असे अपेक्षित उत्तर मिळते. उदाहरणार्थ, z = (3, –4) असेल, तर –z = (–3, 4). या व्याख्येमुळे आता w या संमिश्र संख्येतून z ही संमिश्र संख्या वजा करण्यासाठी w – z = w + (–z) असे सांगितले की काम झाले. उदाहरणार्थ, w = (–2, 5) असेल व z = (3, –4) असेल, तर w – z = (–2, 5) + (–3, 4) = (–5, 9).
संमिश्र संख्यांचा गुणाकार-भागाकार
आता संमिश्र संख्यांच्या गुणाकाराकडे वळू या. बेरजेच्या धर्तीवर z = (x, y) आणि w = (u, v) या संमिश्र संख्यांच्या गुणाकाराची व्याख्या zw = (x, y)(u, v) = (xu, yv) अशी केली, तर (1, 0)(0, 1) = (0, 0) असे समीकरण मिळाले असते, व (1, 0) आणि (0, 1) या दोन (0, 0) नसलेल्या संख्यांचा गुणाकार (0, 0) होऊन पंचाइत झाली असती; दुसरे असे की z = (x, y) या कुठल्याही संमिश्र संख्येचा वर्ग z2 = (x2, y2) असा झाला असता, व तो कधीच (–1, 0) या वास्तव संख्येच्या बरोबर झाला नसता, आणि आपला संमिश्र संख्यांकडे वळण्याचा हेतूच बारगळला असता.
आता z = (x, y) आणि w = (u, v) या संमिश्र संख्यांचा गुणाकार कसा करायचा हे ठरवण्यासाठी प्रथम आपण x + yt आणि u + vt या रेषीय पदावलींचा (polynomials of degree 1) गुणाकार करून पाहू या. तो असा होतो :
आपण t2 + 1 = 0 हे समीकरण सोडवू इच्छित असल्याने वरील समानतेत (equality) t2 = -1 घालणे उचित आहे, व त्यामुळे आपल्याला
अशी समानता मिळते. यामुळे z = (x, y) आणि w = (u, v) या संमिश्र संख्यांच्या गुणाकाराची व्याख्या
अशी करणे उचित होते. उदाहरणार्थ, (2, 3)(3, 1) = (6 – 3, 2 + 9) = (3, 11). तसेच zz = (xx – yy, xy + yx), म्हणजेच z2 = (x2 – y2, 2xy) असा z या संमिश्र संख्येचा वर्ग होतो. त्यामुळे x आणि y या वास्तव संख्यांसाठी
अशी उत्तरे मिळतात. विशेषतः, z = (0, 1) या कल्पित संख्येचा वर्ग z2 = (–12, 0) = –1 असा होतो, व आपण शोधत असलेले t2 + 1 = 0 या समीकरणाचे (0, 1) हे उत्तर मिळून जाते. अशाप्रकारे (0, 1) ही कल्पित संख्या आपल्याला मिळाली आहे की जिचा वर्ग –1 आहे.
गुणाकार करता आला तसा भागाकारही करता आला पाहिजे. समजा z = (x, y) ही संमिश्र संख्या (0, 0) नाही, म्हणजे x आणि y या दोन्ही वास्तव संख्या 0 नाहीत, आणि म्हणून x2 + y2 ही वास्तव संख्या 0 नाही. आपल्याला 1/z = (u, v) ही अशी संमिश्र संख्या हवी आहे की z(1/z) = 1, म्हणजेच (xu - yv, yu + xv) = (1, 0), हे उत्तर मिळेल. आता xu – yv = 1 आणि yu + xv = 0 या दोन समीकरणांपैकी पहिल्याला y ने आणि दुसऱ्याला x गुणून, त्यांची बेरीज केली तर (x2 + y2)u = x असे, व त्यांची वजाबाकी केली तर (x2 + y2)v = -y असे उत्तर मिळते, म्हणजेच u = x/(x2 + y2) आणि v = –y/(x2 + y2) अशी उत्तरे मिळतात.

उदाहरणार्थ, z = (3, –4) असेल, तर 1/z = (3/(32 + 42), 4/(32 + 42)) = (3/25, 4/25). आता z ही संमिश्र संख्या (0, 0) नसेल, व आपल्याला w या संमिश्र संख्येला z या संख्येने भागायचे असेल, तर w/z = w(1/z) असे सांगितले की काम झाले. उदाहरणार्थ, w = (–2, 5) असेल व z = (3, –4) असेल, तर w/z = (–2, 5) (3/25, 4/25) = (–26/25, 7/25).
(0, 1) ही कल्पित संख्या सर्वसामान्यपणे i या चिह्नाने दाखवतात, व म्हणून i2 = –1 असे लिहितात. समजा x आणि y या वास्तव संख्या आहेत. आपल्या गुणाकाराच्या नियमाप्रमाणे (0, 1)(y, 0) = (0, y) आणि म्हणून (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0). याचा अर्थ असा की आपण z = (x, y) ही कुठलीही संमिश्र संख्या x + i y याप्रकारे लिहू शकतो. फक्त i2 = -1 एवढे लक्षात ठेवले की z = (x, y) आणि w = (u, v) या संमिश्र संख्यांची बेरीज (x + i y) + (u + i v) = (x + u) + i (y + v) अशी व व त्यांचा गुणाकार (x + i y) (u+ i v) = (xu - yv) + i (xv + yu) असा नेहमीच्या पद्धतीने करणे सोपे जाते. गुणाकाराची आधी दिलेली गुंतागुंतीची व्याख्या आता बाजूला ठेवली तरी चालेल.
ज्यांनी या आधी संमिश्र संख्या z = x + i y या स्वरूपात बघितल्या असतील, आणि i या संख्येचा वर्ग -1 होतो असे मानून अंकगणितातील सर्व क्रिया केल्या असतील त्यांना कदाचित वाटेल की हीच गोष्ट साधण्यासाठी आपण केलेला खटाटोप म्हणजे डोंगर पोखरून उंदीर काढण्यासारखे झाले. या खटाटोपाचे कारण गणित या विषयाच्या स्वरूपात दडलेले आहे. गणितात कुठल्याही गोष्टीचे नुसते गुणधर्म सांगून व तिचा उपयोग कसा करायचा एवढेच सांगून पुरत नाही. प्रथम त्या गोष्टीची व्याख्या द्यावी लागते, ती गोष्ट अस्तित्वात आहे असे दाखवावे लागते, व नंतरच तिचे गुणधर्म तपासता येतात. आपण i म्हणजे (0, 1) ही कल्पित संख्या होय अशी व्याख्या केली, व नंतर कल्पित संख्यांसाठी लागू पडणाऱ्या नियमांप्रमाणे तिचा वर्ग -1 होतो असे दाखवून दिले. हे करण्यासाठी आपल्याला प्रयास पडले खरे, पण पाया पक्का झाला.
z = (x, y) या बिंदूचे (0, 0) या बिंदूपासूनचे जे अंतर आहे, त्याला z या संख्येचे केवल मूल्य (absolute value) असे म्हणतात, व ते |z| या चिह्नाने दाखवतात. पायथागोरसच्या सिद्धांतानुसार |z|2 = x2 + y2 असे मिळते, व म्हणून |z| = (x2 + y2)½ अशी व्याख्या करता येते. समजा z = (x, y) हा (0, 0) पेक्षा वेगळा बिंदू आहे. z व (0, 0) या दोन बिंदूंना जोडणारी रेषा, (1, 0) व (0, 0) या दोन बिंदूंना जोडणाऱ्या रेषेशी जो कोन करते (जास्तीत जास्त 180° चा, पण –180° पेक्षा मोठा), त्याला z या संख्येचा कोनांक (argument) असे म्हणतात, व तो arg(z) या चिह्नाने दाखवतात. जसा z = (x, y) हा बिंदू x आणि y या दोन निर्देशकांनी निश्चित होतो, तसा |z| आणि arg(z) यांनीही निर्धारित होतो. खालील आकृतीच्या डाव्या भागात |z| आणि arg(z) चित्रित केले आहेत.
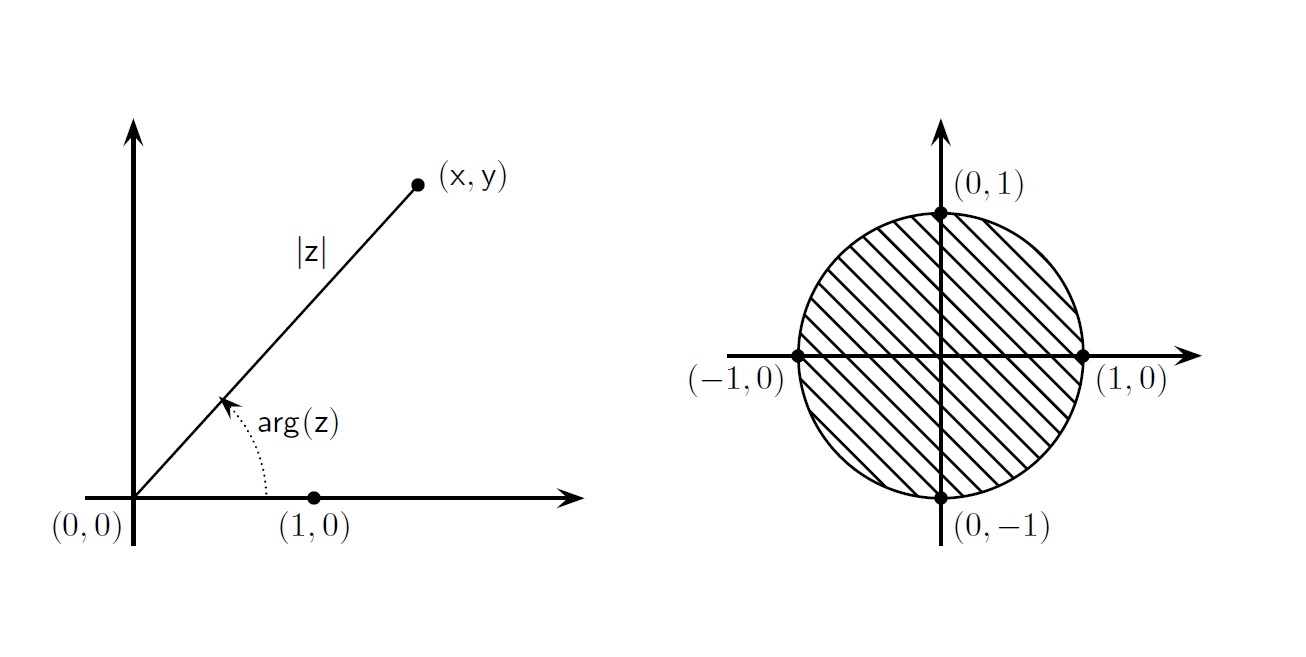
ज्या बिंदूंचे अंतर (0, 0) पासून 1 पेक्षा कमी आहे अशा सर्व बिंदूंची एक चकती (disk) बनते. तिची त्रिज्या 1 असल्याने तिला एककी (unit) म्हणतात. ज्यांचे केवल मूल्य (absolute value) 1 आहे अशा सर्व संमिश्र संख्या या चकतीच्या काठावर असतात, पण त्यांचा या चकतीत समावेश होत नाही, म्हणून ती चकती विवृत (open) आहे असे म्हटले जाते. अशी ही विवृत एककी चकती (open unit disk) वरील आकृतीच्या उजव्या भागात तिरक्या रेघांनी दाखवली आहे.
गुणाकाराच्या व्याख्येचा भूमितीच्या दृष्टीने असा अर्थ लावता येतो: z = (x, y) व (0, 0) या दोन बिंदूंना जोडणाऱ्या रेषेची लांबी |z| आहे, आणि ती रेषा (1, 0) व (0, 0) या दोन बिंदूंना जोडणाऱ्या रेषेशी arg(z) अंशांचा कोन करते; तसेच w = (u, v) व (0, 0) या दोन बिंदूंना जोडणाऱ्या रेषेची लांबी |w| आहे, व ती रेषा (1, 0) व (0, 0) या दोन बिंदूंना जोडणाऱ्या रेषेशी arg(w) अंशांचा कोन करते. ज्या बिंदूचे (0, 0) पासूनचे अंतर |z||w| आहे आणि ज्याचा कोनांक तत्त्वतः arg(z) + arg(w) आहे, तो बिंदू z आणि w यांचा गुणाकार दर्शवितो. खालील आकृतीवरून याची कल्पना येईल, पण हे विधान सिद्ध करण्यासाठी त्रिकोणमितीचा (trigonometry) उपयोग करावा लागेल.
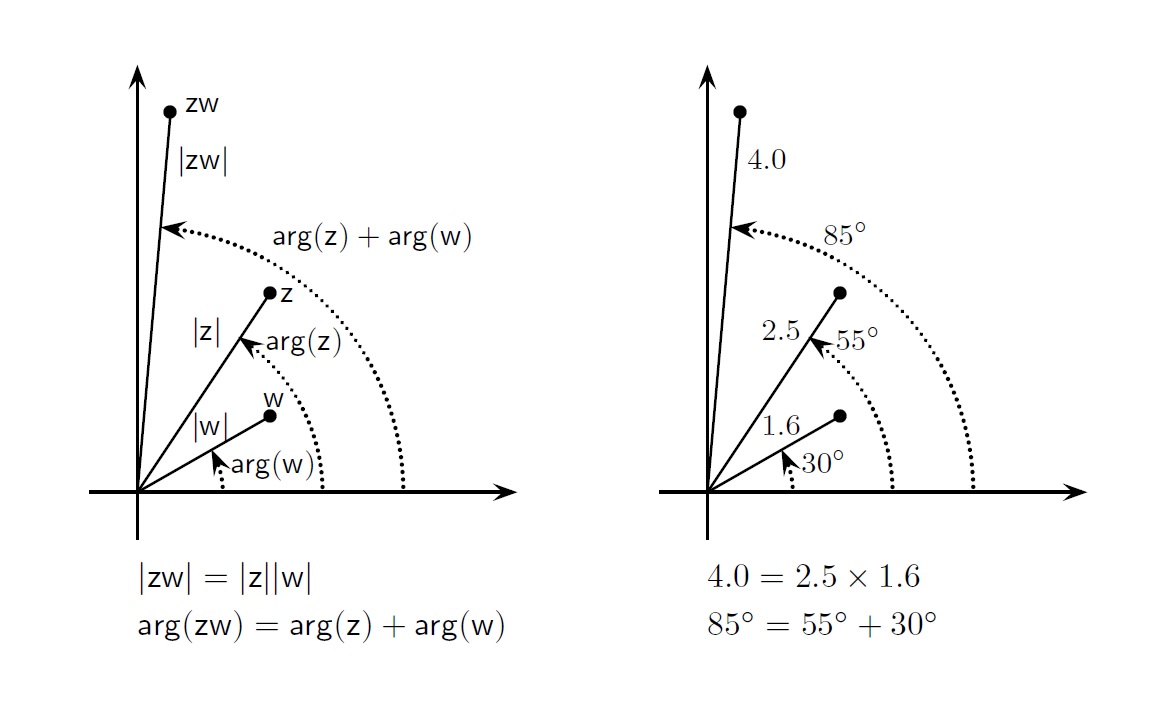
दोन वेगळ्या वास्तव संख्या घेतल्या तर त्यांपैकी एक दुसरीपेक्षा लहान असते, व संख्यारेषेवर लहान संख्या मोठ्या संख्येच्या डावीकडे दाखवली जाते. मात्र असे आपण संमिश्र संख्यांबाबत म्हणू वा दाखवू शकत नाही, म्हणजे दोन वेगळ्या संमिश्र संख्या घेतल्या तर त्यांपैकी लहान कुठली व मोठी कुठली असे काही सांगता येत नाही. आपण फक्त एका संख्येचे केवल मूल्य, म्हणजे तिचे (0, 0) या बिंदूपासूनचे अंतर, दुसऱ्या संख्येच्या केवल मूल्याइतकेच आहे की त्याच्यापेक्षा कमी आहे एवढेच पाहू शकतो. उदाहरणार्थ, z = (3, –4) असेल, तर |z| = (32 + 42)½ = 5, म्हणजे z या संख्येचे केवल मूल्य 5 आहे. आता w = (–2, 5) असेल, तर |w| = (22 + 52)½ = 29½, व म्हणून z या संख्येचे केवल मूल्य w या संख्येच्या केवल मूल्यापेक्षा कमी आहे, पण जर w = (–4, 3) असेल, तर |w| = (42 + 32)½ = 5, व म्हणून z आणि w या संख्यांची केवल मूल्ये समान आहेत.
संमिश्र संख्यांच्या पलीकडे?
आतापर्यंत ज्या निरनिराळ्या संख्यांची आपण ओळख करून घेतली, त्यांचा आढावा घेऊ या. आपण नैसर्गिक संख्या व शून्य यांपासून सुरुवात केली. t + 1 = 0 हे समीकरण सोडवण्यासाठी ऋण पूर्णांकांची जरुरी भासली, तर 2t – 1 = 0 हे समीकरण सोडवण्यासाठी अपूर्णांक आवश्यक ठरले. नंतर t2 – 2 = 0 हे समीकरण सोडवण्यासाठी अपरिमेय संख्या व t2 + 1 = 0 हे समीकरण सोडवण्यासाठी कल्पित संख्या शोधाव्या लागल्या. असे करता करता आपण प्रतलावरील बिंदू दर्शवतात त्या संमिश्र संख्यांपर्यंत येऊन पोचलो. संख्येच्या संकल्पनेचा असा विस्तार करताना प्रत्येक वेळी आपण बेरीज, वजाबाकी, गुणाकार, भागाकार या क्रियांचे नेहमीचे मूलभूत नियम कायम राखले. आता साहजिकच असा प्रश्न उभा राहतो की t2 + t + 1 = 0 किंवा t3 + t2 + t + 1 = 0 अशी वेगवेगळी समीकरणे सोडवण्यासाठी आपल्याला आणखी कुठल्या प्रकारच्या संख्यांची जरूर भासेल का. या प्रश्नाचे आश्चर्यकारक उत्तर असे आहे की यासाठी संख्येच्या संकल्पनेचा अजून विस्तार करावा लागत नाही. या संबंधीच्या सिद्धांताला बीजगणिताचे मूलभूत प्रमेय असे म्हणतात. ते आता सांगतो.
समजा n ही एक नैसर्गिक संख्या आहे, व a0, a1, a2, ..., an या काही संमिश्र संख्या आहेत. संमिश्र संख्यांची बेरीज व त्यांचा गुणाकार या क्रिया पुन्हा पुन्हा वापरून z या कुठल्याही संमिश्र संख्येसाठी आपल्याला
अशी बहुपदी (polynomial) बनवता येते. जर an शून्य नसेल तर p(z) = 0 हे समीकरण सोडवणारी संमिश्र संख्या नेहमीच असते; इतकेच नव्हे तर z1, z2, ..., zn अशा n संमिश्र संख्या असतात की आपण आपली बहुपदी
अशी लिहू शकतो, व त्यामुळे p(z) = 0 ह्या समीकरणाची z1, z2, ..., zn ही उत्तरे बनतात. या n संमिश्र संख्या प्रत्यक्षात कशा शोधून काढयच्या हा वेगळा प्रश्न आहे. जर n = 1 असेल, तर z1 = -a0/a1 असे उत्तर लगेच मिळते, आणि जर n = 2 असेल, तर ही द्विपदी (quadratic) सोडवण्याचे सूत्र खूप जण शाळा-कॉलेजात शिकतात. जर n = 3 असेल किंवा n = 4 असेल, तर अशी सूत्रे उपलब्ध आहेत, पण n > 4 असेल तर असे कोणतेच सर्वसामान्य सूत्र असू शकत नाही. अशा वेळी संगणकाचा उपयोग करून यथार्थ (exact) उत्तरांच्या निकट जाणाऱ्या (approximate) उत्तरांवर खूप वेळा समाधान मानावे लागते. पण संमिश्र संख्यांच्या पलीकडे जावे लागत नाही हे निश्चित.
बीजगणिताच्या मूलभूत प्रमेयाची पहिली तर्कशुद्ध सिद्धता ज्याँ रोबेर आर्गान (Jean-Robert Argand) या होतकरु गणितज्ञाने 1814 साली दिली. तो पॅरिसमध्ये एक पुस्तकांचे दुकान चालवत असे. हीच सिद्धता प्रख्यात फ्रेंच गणिती ओगस्तँ लुइ कोशी (Augustin Louis Cauchy) याने 1821 साली लिहिलेल्या आपल्या पाठ्यपुस्तकात दिली, पण आर्गानचा नामोल्लेख केला नाही. पूर्वी बीजगणित (algebra) म्हणजे समीकरणांचा सिद्धांत (theory of equations) असे मानले जात असल्याने या प्रमेयाला बीजगणिताचे मूलभूत प्रमेय हे नाव मिळाले. परंतु आतापर्यंत त्याची कुठलीही सिद्धता फक्त बीजगणित वापरून दिलेली नाही; प्रत्येक सिद्धतेत कुठे ना कुठे गणिती विश्लेषण (mathematical analysis) डोकावतेच. या प्रमेयामुळे बहुपदींची समीकरणे सोडवण्यासाठी चाललेला नवनवीन संख्यांचा शोध संमिश्र संख्यांपाशी थांबला, व संख्याविश्वाला एक प्रकारची पूर्णता आली. ऑयलर (Leonhard Euler) या गणितज्ञाने अठराव्या शतकात संमिश्र संख्याबाबत पायाभूत काम केले. -1च्या वर्गमूळासाठी i हे चिह्न त्याच्यामुळेच प्रचलित झाले, व त्यानेच 0, 1, e , π (पाय) आणि i या महत्त्वपूर्ण संख्यांना एकत्र आणणारे eiπ + 1 = 0 हे समीकरण मांडले.
वास्तव संख्यांचा विस्तार करून संमिश्र संख्या मिळवताना वास्तव संख्यांच्या गुणाकाराबाबतचे आपण नकळत नेहमी वापरत असलेले गुणधर्म टिकून रहातात, जसे (१) (z + w)t = zt + wt, t(z + w) =tz + tw, (२) zw = 0 असेल तर z = 0 किंवा w = 0, (३) z(wt) = (zw)t (साहचर्य, associativity), (४) zw = wz (क्रमनिरपेक्षता, commutativity). आता संमिश्र संख्यांचा विस्तार करायचा म्हटला आणि गुणाकाराचे हे चारही गुणधर्म टिकून ठेवायचे ठरवले, तर ते शक्य नाही. पण गुणाकाराचा वरीलपैकी फक्त चौथा, म्हणजे क्रमनिरपेक्षता हा गुणधर्म नसला तरी चालेल असे मानले, तर आपल्याला चतुर्दल संख्या (quaternions) मिळतात. कुठलीही संमिश्र संख्या जशी दोन वास्तव संख्यांची एक जोडी असते, तशी कुठलीही चतुर्दल संख्या दोन संमिश्र संख्यांची एक जोडी असते. यापुढे जाऊन, गुणाकाराचा वरीलपैकी तिसरा, म्हणजे साहचर्य हा गुणधर्म देखील नसला तरी चालेल असे मानले, तर आपल्याला अष्टदल संख्या (octonions) मिळतात; कुठलीही अष्टदल संख्या दोन चतुर्दल संख्यांची एक जोडी असते. त्यामुळे वास्तव संख्यांची मिति (dimension) 1 असेल, तर संमिश्र संख्यांची मिति 2, चतुर्दल संख्यांची मिति 4 आणि अष्टदल संख्यांची मिति 8 होते. बस्स, एवढेच; वर दिलेले गुणाकाराचे पहिले दोन गुणधर्म बाळगणाऱ्या यांच्यापेक्षा अधिक संख्या मिळू शकत नाहीत.
उच्च स्तरावरील गणिताच्या कित्येक भागात संमिश्र संख्यांचा उपयोग अनिवार्य आहे. प्राध्यापक रवीन्द्र बापट यांनी ‘ऐसी प्रमेये रसिके’ या त्यांच्या पुस्तकात संमिश्र संख्यांना आजच्या गणितज्ञाची मूलभूत गरज किंवा ‘कच्चा माल’ असे संबोधले आहे!
---
बालमोहन लिमये
(balmohan.limaye@gmail.com)

लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.
बालमोहन लिमये यांचे इतर लिखाण


प्रतिक्रिया
Name of the book by Prof. Ravindra Bapat
Respected Sir, It's indeed an excellent article.
I may be wrong, but the name of the book by Prof. Ravindra Bapat is ऐसी प्रमेये रसिके.
आभार
बदल केला आहे.
वा वा.
मला Shaum series चं नंबर लाइन ( असंच काही नाव होतं) (१९७२)वाचल्याचं आठवलं. जाडजुड आणि जड पुस्तक होतं.
कोणतीही गोष्ट समजावण्याची घाई नसलेलं पुस्तक.
रिडक्षिओ ॲड ॲब्सर्डम्
Proof by contradiction ह्मणजेच reductio ad absurdum कां?
….शेवटी मदांध तख्त फोडते मराठी!
ही पद्धत ग्रीक
तत्त्ववेत्त्यांनी प्रथम बाजारात आणली. (असं वाचलंय. तेव्हा मी नव्हतो. )
उत्तम आढावा
नैसर्गिक संख्यांपासून प्रारम्भ करून आवश्यकतेनुसार ह्रस्व संख्या, अपूर्णांक, इत्यादि संख्या निर्माण करत गणितशास्त्र संमिश्र संख्यांपर्यंत कसे पोहोचले आणि हे साधतांना नैसर्गिक संख्यांच्या Cumulative, Associative, Distributive आणि Identity ह्य वैशिष्ट्यांना कसे जपले आहे ह्याचा हा उत्तम आढावा बालमोहन लिमये ह्यांनी आपल्या समोर ठेवला आहे.
ऑयलरचे 0, 1, e , π (पाय) आणि i या महत्त्वपूर्ण संख्यांना एकत्र आणणारे eiπ + 1 = 0 हे समीकरण शिकवितांना आमचे गणिताचे प्राध्यापक एन आर कुलकर्णी ह्यांनी शेवटची पायरी म्हणून हे समीकरण फळ्यावर लिहिले तेव्हा अंधाऱ्या बोगद्यातून अचानक उजेडात आल्यावर जसे डोळे दिपतात तीच अनुभूति मला आणि माझ्या शेजारी बसलेल्या श्री मा भावे ह्यांना झाल्याचे चांगले आठवते.
ह्याच समीकरणाबाबत माझे मित्र अनिल खर्शीकर ह्यांच्याशी अलीकडे बोललो तेव्हा त्यांनी ह्या समीकरणाबाबत "A Most Elegant Equation - Euler’s Formula and the Beauty of Mathematics" ह्या David Stipp लिखित पुस्तकाचा उल्लेख केला. ते जालावरून मला मिळाले आहे आणि सावकाशीने मी ते वाचत आहे.
ओयलरने हा शोध कसा लावला?
ओयलर आणि न्युटन जबरी गणिती होते. आणखी बरेच आहेत पण जरा हे अधिक आवडतात.
बैजिक (algebraic) संख्या
काही वाचकांनी विचारल्यावरून वास्तव संख्यांची विभागणी बैजिक (algebraic) संख्या आणि अबैजिक (transcendental) संख्या यांत कशी करतात हे दाखवणारा एक नवीन परिच्छेद लेखात समाविष्ट केला आहे.
संख्यांच्या दुनियेत
संख्यांच्या दुनियेत
संख्यांच्या दुनियेत फारच छान लेख.
संमिश्र संख्या शिकून चार पाच गुण
मिळवले आणि त्याच्या योगदानावर
गणितात पास झालो. तेंव्हा या लेखातील
शब्द माहित झाले पण संकल्पना शून्यच.
तेंव्हाच हे सर्व कळले असते तर?
या संकल्पना शिकवणे महत्वाचे की
त्यावर आधारित गणित शिकवणे हे
प्राध्यापकांनीच आणि शिक्षण तज्ञांनी
ठरवायचे आहे. मला पहिला पर्याय
महत्वाचा वाटतो.
वसंत साठये