गणिताच्या निमित्ताने - भाग ६ [चार रंग पुरेसे आहेत]
गणिताच्या निमित्ताने – भाग ६ [चार रंग पुरेसे आहेत]
बालमोहन लिमये
(नकाशा रंगवण्यासाठी पाच रंग पुरतात हे आपण मागील भागात पाहिले. पण चारच रंग पुरू शकतात यासाठी लागणारा युक्तिवाद जाणून घेण्याचे कुतूहल असणे साहजिक आहे. प्रत्यक्ष गणित वाचले नाही, तरी गणितज्ञ कशाप्रकारे युक्तिवाद करतात हे जाणून घेण्यासाठी – प्राध्यापक बालमोहन लिमये यांच्या साप्ताहिक लेखमालेतील पुढील भाग. मागील भाग इथे.)
चार रंग पुरेसे आहेत
नकाशातील शेजारच्या प्रदेशांना वेगळे रंग द्यायचे ठरवले तर तीन रंग पुरत नाहीत, पण पाच रंग पुरतात हे आपण पाहिले; खरे म्हणजे चार रंग पुरतात असे दाखवायचे होते, पण ते शक्य झाले नाही. त्याचे काय कारण होते, आपली गाडी कुठपर्यंत आली व कशामुळे अडकून पडली ते परत एकदा पाहू या, म्हणजे त्यातून मार्ग कसा निघू शकतो ते समजून येईल.
प्रतल आलेखातील (plane graph) शिरोबिंदूंना (vertices) रंग द्यायचे, मात्र दोन शिरोबिंदू एकमेकांचे शेजारी (neighbours) असतील तर त्यांचे रंग वेगळे असले पाहिजेत अशी काळजी घ्यायची. याला उचित रंगकाम म्हटले जाते. आपण क्षणभर असे समजू या की चार रंग वापरून असे उचित रंगकाम करणे नेहमीच शक्य नाही. मग एक तरी प्रतल आलेख असा असेल की ज्यासाठी पाच रंगांची जरुरी आहे. अशा आलेखाला प्रत्युदाहरण (counter example) असे म्हणतात. अशा प्रत्युदाहरणांपैकी ज्या आलेखात कमीत कमी शिरोबिंदू असतील अशा कुठल्याही प्रत्युदाहरणाला किमान स्वरुपाचे प्रत्युदाहरण असे म्हणतात. जर किमान स्वरुपाच्या प्रत्युदाहरणातील एक बिंदू वगळला (आणि त्यापासून निघणाऱ्या कडा देखील), तर उरलेल्या आलेखात किमान स्वरुपाच्या प्रत्युदाहरणातील शिरोबिंदूंपेक्षाही एक शिरोबिंदू कमी असतो, व म्हणून तो आलेख प्रत्युदाहरणच नाही, म्हणजेच उरलेला आलेख चार रंग वापरून उचित प्रकारे रंगवता येतो.
किमान स्वरुपाच्या प्रत्युदाहरणातील वगळलेला शिरोबिंदू 1, 2, 3 किंवा 4 कोटीचा असेल आणि उरलेल्या आलेखातील शिरोबिंदू आपण चार रंग वापरून उचित रीतीने रंगवले तर वगळलेला बिंदू परत घातल्यावरही आपण सगळा आलेख चार रंग वापरून उचित रीतीने कसा रंगवता येतो, व त्यामुळे तो आलेख प्रत्युदाहरण असू शकत नाही हे देखील आपण पाहिले. याचाच अर्थ असा की किमान स्वरुपाच्या प्रत्युदाहरणातील कुठलाही शिरोबिंदू 1, 2, 3 किंवा 4 कोटीचा नसतो. जर हीच गोष्ट आपण 5 कोटीच्या शिरोबिंदूसाठी सिद्ध करु शकलो असतो तर आपले काम फत्ते झाले असते, कारण ऑयलरच्या सूत्रानूसार कुठल्याही प्रतल आलेखात एक तरी बिंदू जास्तीतजास्त 5 कोटीचा असतो, व तो वगळून व नंतर त्याला परत घालून चार रंगांचे उचित रंगकाम करता आले असते, म्हणजे घेतलेला आलेख प्रत्युदाहरणच राहिला नसता. ह्या विसंगतीमुळे आपण ठामपणे म्हणू शकलो असतो की प्रत्येक प्रतल आलेख उचित प्रकारे रंगवायला चार रंग पुरतात. पण 5 कोटीचा शिरोबिंदू वगळून रंगकाम केल्यावर व तो परत घातल्यावर चारच रंग पुरू शकतात असे आपण दाखवू शकत नाही, व म्हणून आपली गाडी तिथेच अडकून पडते.
या गाडीला पुढे नेण्यासाठी दोन गोष्टी करणे जरूर ठरते. पहिली म्हणजे किमान स्वरुपाच्या प्रत्युदाहरणातून एकाऐवजी अनेक शिरोबिंदूंचा संच (set) वगळून चार रंग वापरून उचित रंगकाम करायचे, नंतर तो संच परत घालायचा व पूर्ण आलेख चार रंग वापरून उचित प्रकारे रंगवता येतो का हे पहायचे. दुसरी म्हणजे शिरोबिंदूंचे असे काही आकृतिबंध शोधायचे की कुठल्याही प्रतल आलेखात त्यांपैकी एक तरी आकृतिबंध असला पाहिजे. या दोन गोष्टींचा योग्य मिलाफ करता आला तर आपली गाडी मुक्कामावर पोचू शकते. याबाबत आता सविस्तर चर्चा करु या.
प्रतल आलेखातील एक किंवा अनेक शिरोबिंदूंच्या कोटींचा निर्देश करून ते एक-दुसऱ्याशी कसे जोडले जातात हे दाखवणाऱ्या शिरोबिंदूंच्या रचनेला आकृतिबंध (configuration) असे म्हणतात. उदाहरणार्थ, आकृती १ (अ) मध्ये तांबड्या रंगाने दाखवलेला 4 कोटीचा एक शिरोबिंदू हा आकृतिबंध आहे. तसेच आकृती १ (ब) मध्ये तांबड्या रंगाने दाखवलेल्या 5 कोटीच्या एकमेकांना जोडलेल्या तीन शिरोबिंदूंचा त्रिकोण हासुद्धा आकृतिबंध आहे.

आकृती १ (अ) - डावीकडे आकृती १ (ब) - उजवीकडे
एखादा आकृतिबंध आलेखातून वगळायचा असेल तर आपण एक शिरोबिंदू वगळताना जे करतो तेच करायचे, म्हणजे त्या आकृतिबंधात असणारे सर्व शिरोबिंदू व त्यांच्यापासून निघणाऱ्या सर्व कडा गाळून टाकायच्या. उदाहरणार्थ, आकृती १ (अ) व आकृती १ (ब) मध्ये दाखवलेल्या तांबड्या रंगांच्या आकृतिबंधांतील शिरोबिंदू व त्यांपासून निघणाऱ्या कडा आकृती २ (अ) व आकृती २ (ब) मध्ये तांबड्या रंगानेच दाखवल्या आहेत. तसेच ते दोन आकृतिबंध वगळल्यावर उरणारे आलेख आकृती ३ (अ) व आकृती ३ (ब) मध्ये दाखवले आहेत.
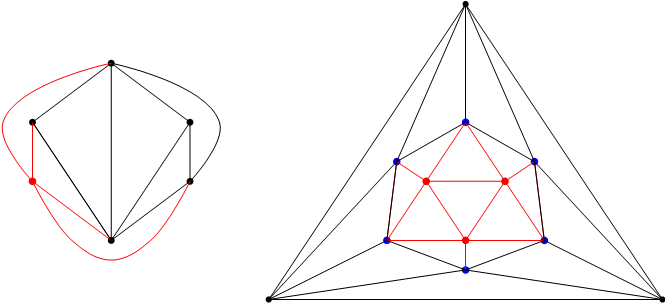
आकृती २ (अ) - डावीकडे आकृती २ (ब) - उजवीकडे

आकृती ३ (अ) - डावीकडे आकृती ३ (ब) - उजवीकडे
किमान स्वरूपाच्या प्रत्युदाहरणातून 5 कोटीचा एक शिरोबिंदू वगळून काम भागत नसल्याने अनेक शिरोबिंदूंचा आकृतिबंध वगळला तर मागील लेखात दिलेल्या आल्फ्रेड ब्रे केम्प या गणितज्ञाच्या युक्तिवादासारखा काही युक्तिवाद करता यावा असा विचार जॉर्ज डी. बिरकॉफ (George D. Birkhoff) या अमेरिकन गणितज्ञाने मांडला, ‘The reducibility of maps’ या शोधनिबंधामध्ये १९१३ साली.
जर एखादा आकृतिबंध कुठल्याही किमान स्वरूपाच्या प्रत्युदाहरणाचा भाग होऊ शकत नसेल तर त्याला वगळण्याजोगा आकृतिबंध (reducible configuration) असे नाव बिरकॉफने दिले. याचा अर्थ असा की किमान स्वरूपाच्या प्रत्युदाहरणातून अशा आकृतिबंधाला वगळल्यावर उरलेल्या आलेखातील शिरोबिंदू चार रंग वापरून उचित रीतीने कसेही रंगवले, व त्या रंगांत जरूर ते बदल केले, तर त्या रंगसंगतीचा विस्तार (extension) करून संपूर्ण आलेखाचे शिरोबिंदू चार रंग वापरून उचित रीतीने रंगवता येतात, व त्यामुळे तो आलेख प्रत्युदाहरण होऊ शकत नाही. आपण वगळण्याजोग्या आकृतिबंधाची चार उदाहरणे पाहिली आहेत; ती म्हणजे 1 कोटीचा एक शिरोबिंदू, 2 कोटीचा एक शिरोबिंदू, 3 कोटीचा एक शिरोबिंदू, व 4 कोटीचा एक शिरोबिंदू. यांपैकी पहिले तीन आकृतिबंध कसे वगळण्याजोगे आहेत ते आपण एका फटक्यात दाखवले होते. चौथा आकृतिबंध कसा वगळण्याजोगा आहे ते दाखवण्यासाठी केम्पच्या साखळीचा वापर करावा लागतो याबद्दलही आपण चर्चा केली आहे. जर 5 कोटीचा एक शिरोबिंदू हा आकृतिबंधदेखील वगळण्याजोगा आहे असे केम्पला दाखवता आले असते तर चार रंगांचे प्रमेय सिद्ध झाले असते हेही आपण बघितले आहे.

जॉर्ज बिरकॉफ
आता बिरकॉफने सुचवलेले एका विशिष्ट प्रकारचे आकृतिबंध जाणून घेऊ. प्रतल आलेखातील काही शिरोबिंदू एक वलय (ring) बनवतात याचा अर्थ असा की जर त्या शिरोबिंदूंची चक्रीय गणना केली तर त्यांपैकी प्रत्येक शिरोबिंदू त्याच्या आधीच्या व त्याच्या नंतरच्या शिरोबिंदूंचा शेजारी असतो, पण वलयातील इतर कुणाचा शेजारी नसतो. वलयाच्या अंतर्भागातील शिरोबिंदू एकमेकांचे शेजारी असू शकतात, व तसेच वलयाच्या बाह्यभागातील शिरोबिंदू एकमेकांचे शेजारी असू शकतात, पण अंतर्भागातील कुठलाही शिरोबिंदू बाह्यभागातील शिरोबिंदूचा शेजारी असू शकत नाही. त्यामुळे त्या आलेखाचा आपण दोन स्वतंत्ररीत्या विचार करू शकतो.
आलेखातील तीन शिरोबिंदूंपैकी जर प्रत्येक शिरोबिंदू इतर दोघांचा शेजारी असेल तर ते तीन शिरोबिंदू नक्कीच एक वलय बनवतात. बिरकॉफने नमूद केले की अशा तीन शिरोबिंदूंनी बनलेल्या (त्रिकोणी) वलयाच्या अंतर्भागात किमान एक शिरोबिंदू असेल व त्याच्या बाह्यभागातही किमान एक शिरोबिंदू असेल, तर त्या वलयाच्या अंतर्भागातील सर्व शिरोबिंदूंनी बनणारा आकृतिबंध वगळण्याजोगा असतो, मग ते शिरोबिंदू कोणत्या का कोटीचे असेनात. उदाहरणार्थ, आकृती ४ मध्ये निळ्या रंगाने दाखवलेल्या (त्रिकोणी) वलयाच्या बहिर्भागात 4 कोटीचे तीन शिरोबिंदू आहेत, तर त्याच्या अंतर्भागातील सहा शिरोबिंदूंपैकी एक शिरोबिंदू 7 कोटीचा, एक शिरोबिंदू 6 कोटीचा, व चार शिरोबिंदू 4 कोटीचे आहेत. अंतर्भागातील सहा शिरोबिंदूंनी बनवलेला आकृतिबंध तांबड्या रंगाने दाखवला आहे.
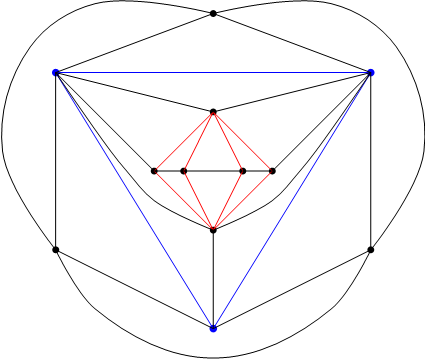
आकृती ४
बिरकॉफच्या विधानानुसार हा तांबड्या रंगाने दाखवलेला आकृतीबंध वगळण्याजोगा आहे. याचे कारण असे आहे : समजा हा आकृतिबंध एका किमान स्वरूपाच्या प्रत्युदाहरणाचा भाग आहे. मग या (त्रिकोणी) वलयाच्या अंतर्भागात एक तरी शिरोबिंदू असल्याने तो अंतर्भाग वगळून उरलेल्या आलेखातील शिरोबिंदू तांबडा, निळा, पिवळा व हिरवा हे चार रंग वापरून उचित रीतीने रंगवता येतात. वलयातील तीन शिरोबिंदू एकमेकांचे शेजारी असल्याने या रंगकामात त्यांना तीन वेगवेगळे रंग मिळणार; समजा तांबडा, निळा व पिवळा. त्याचप्रमाणे वलयाच्या बाह्यभागात एक तरी शिरोबिंदू असल्याने तो बाह्यभाग वगळून उरलेल्या आलेखातील शिरोबिंदू तांबडा, निळा, पिवळा व हिरवा हे चार रंग वापरून उचित रीतीने रंगवता येतात. या रंगकामातही आपल्या (त्रिकोणी) वलयातील तीन शिरोबिंदूंना तीन वेगवेगळे रंग मिळणार; समजा ते तीन शिरोबिंदू आधीच्याच क्रमाने घेतले तर त्यांचे रंग आहेत क, च आणि त. जर क हा तांबडा रंग असेल, च हा निळा रंग असेल आणि त हा पिवळा रंग असेल, तर उत्तम. नाही तर, दुसऱ्या वेळी केलेल्या वलय व त्याचा अंतर्भाग यांच्या पुऱ्या रंगकामात क रंगाऐवजी तांबडा रंग, च रंगाऐवजी निळा रंग, त रंगाऐवजी पिवळा रंग, व उरलेल्या चौथ्या रंगाऐवजी हिरवा रंग असा रंगबदल केल्यास दोन्ही रंगकामात (त्रिकोणी) वलयातील तीन शिरोबिंदूंना तेच रंग मिळतात, व संपूर्ण आलेखातील शिरोबिंदू चार रंग वापरून उचित रीतीने रंगवले जातात.
यानंतर बिरकॉफने चार शिरोबिंदूंनी बनलेल्या (चौकोनी) वलयाचा विचार केला. याबाबत जरी आपण त्रिकोणी वलयासाठी केलेला युक्तिवाद करू शकत नसलो, तरी केम्पने प्रस्तुत केलेले एक-आड-एक रंगवलेल्या शिरोबिंदूंच्या साखळीचे तंत्र वापरून बिरकॉफने असे सिद्ध केले की चार शिरोबिंदूंनी बनलेल्या (चौकोनी) वलयाच्या अंतर्भागात किमान एक शिरोबिंदू असेल व त्याच्या बाह्यभागातही किमान एक शिरोबिंदू असेल, तर त्या वलयाच्या अंतर्भागातील सर्व शिरोबिंदूंनी बनणारा आकृतिबंधदेखील वगळण्याजोगा असतो. यापुढे जाऊन पाच शिरोबिंदूंनी बनलेल्या (पंचकोनी) वलयाच्या बाबतीत मात्र असे सर्वसामान्य विधान त्याला करता आले नाही. पंचकोनी वलय बनवणाऱ्या पाच शिरोबिंदूंपैकी प्रत्येक शिरोबिंदू 5 कोटीचा असेल व वलयाच्या अंतर्भागात 5 कोटीचा एकच शिरोबिंदू असेल, तर तो शिरोबिंदू वगळण्याजोगा आहे असे बिरकॉफ सिद्ध करू शकला नाही. हाच प्रश्न केम्पच्या काळापासून चौतीस वर्षे अनिर्णित राहिला होता. हा अजूनही हुलकावणी देणारा आकृतिबंध आकृती ५ (अ) मध्ये दाखवला आहे.
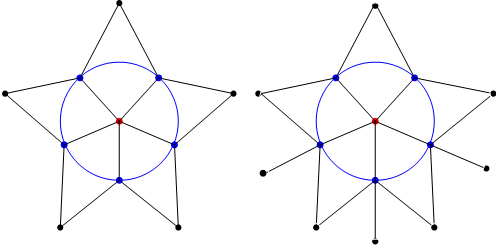
आकृती ५ (अ) - डावीकडे आकृती ५ (ब) - उजवीकडे
नंतर सुमारे दहा वर्षांनी म्हणजे १९२२ साली फिलिप फ्रँकलिन (Philip Franklin) या अमेरिकन गणितज्ञाने सिद्ध केले की पंचकोनी वलयातील पाच शिरोबिंदूंपैकी दोन शिरोबिंदू 5 कोटीचे व तीन शिरोबिंदू 6 कोटीचे असतील, आणि त्याच्या अंतर्भागात 5 कोटीचा एकच शिरोबिंदू असेल तर मात्र तो शिरोबिंदू वगळण्याजोगा असतो. हा आकृतिबंध आकृती ५ (ब) मध्ये दाखवला आहे.
स्वतः बिरकॉफने प्रत्येकी 5 कोटीच्या सहा शिरोबिंदूंनी बनलेल्या (षटकोनी) वलयाच्या अंतर्भागात 5 कोटीचे चार शिरोबिंदू असतील, तर त्या चार शिरोबिंदूंचा आकृतिबंध वगळण्याजोगा असतो असे सिद्ध करून दाखवले. आकृती ६ मध्ये दाखवलेला हा आकृतिबंध बिरकॉफचा हिरा (Birkhoff’s Diamond) या नावाने ओळखला जातो.
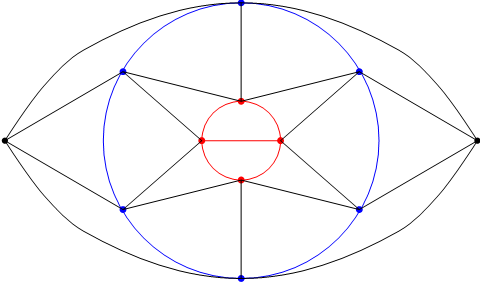
आकृती ६: बिरकॉफचा हिरा
आकृती ६ मधील आलेखात प्रत्येकी 5 कोटीच्या सहा शिरोबिंदूंनी बनलेले (षटकोनी) वलय निळ्या रंगाने दाखवले आहे. त्या वलयाच्या अंतर्भागातील प्रत्येकी 5 कोटीच्या चार शिरोबिंदूंचा आकृतिबंध तांबड्या रंगाने दाखवला आहे. ह्या चार शिरोबिंदूंपैकी आडव्या रेषेने जोडलेले दोन शिरोबिंदू एक-दुसऱ्याच्या मागे-पुढे नसूनही एकमेकांचे शेजारी आहेत, व म्हणून ह्या चार शिरोबिंदूंचे मात्र वलय बनत नाही हे लक्षात घेण्यासारखे आहे.
बिरकॉफने केलेली ही सुरुवात महत्त्वपूर्ण होती. इतर गणितज्ञांनीही अनेक वगळण्याजोगे आकृतिबंध शोधून काढले. आपण पाहिले आहे की ऑयलरच्या एका सूत्रानुसार प्रत्येक प्रतल आलेखात एक तरी शिरोबिंदू असा असतो की ज्याची कोटी जास्तीत जास्त 5 आहे. असा 5 कोटीचा शिरोबिंदू वगळता येत नसल्याने हे सगळे उपदव्याप चालले होते. परंतु चार रंगांच्या अनुमानाची विरोधजन्य सिद्धता देण्यासाठी इतके आकृतिबंध शोधून काढणे जरूर होते की प्रत्येक प्रतल आलेखात त्यांपैकी एक तरी आकृतिबंध समाविष्ट असेल. अशा आकृतिबंधांच्या संचाला अपरिहार्य संच (unavoidable set) असे म्हणू या. उदाहरणार्थ, ऑयलरच्या सूत्रामुळे 1 कोटीचा एक शिरोबिंदू, 2 कोटीचा एक शिरोबिंदू, 3 कोटीचा एक शिरोबिंदू, 4 कोटीचा एक शिरोबिंदू, आणि 5 कोटीचा एक शिरोबिंदू ह्या पाच आकृतिबंधांचा अपरिहार्य संच बनतो. १९०७ साली पॉल वेर्निके (Paul Wernicke) या जर्मन गणितज्ञाने सहा आकृतिबंधांचा आणखी एक अपरिहार्य संच प्रस्तुत केला: 1 कोटीचा एक शिरोबिंदू, 2 कोटीचा एक शिरोबिंदू, 3 कोटीचा एक शिरोबिंदू, 4 कोटीचा एक शिरोबिंदू, 5 कोटीचे एकमेकांचे शेजारी असणारे दोन शिरोबिंदू, आणि 5 कोटीचा एक व 6 कोटीचा एक असे एकमेकांचे शेजारी असणारे दोन शिरोबिंदू. परंतु या यादीतील शेवटचे दोन आकृतिबंध वगळण्याजोगे आहेत असे दाखवता न आल्याने या अपरिहार्य संचानेही काम भागले नाही.
आपण जर वगळण्याजोग्या आकृतिबंधांचा एक अपरिहार्य संच मिळवला तर मात्र चार रंगांच्या अनुमानाची सिद्धता देता येते. ती अशी : समजा S हा एक वगळण्याजोग्या आकृतिबंधांचा अपरिहार्य संच आपण शोधून काढला आहे. ‘प्रतल आलेखातील शिरोबिंदू उचित रीतीने रंगवण्यासाठी चार रंग पुरतात’ हे विधान खोटे असेल तर एका तरी प्रतल आलेखातील शिरोबिंदू चार रंग वापरून उचित रीतीने रंगवता येणार नाहीत. अशा आलेखांपैकी कमीत कमी शिरोबिंदू असलेला एक आलेख निवडून त्याला A असे नाव देऊ या. आकृतिबंधांचा S हा संच अपरिहार्य असल्याने S मधील एक तरी आकृतिबंध A या आलेखात असला पाहिजे. हा आकृतिबंध वगळण्याजोगा असणार कारण S मधील प्रत्येक आकृतिबंध वगळण्याजोगाच आहे. पण किमान स्वरूपाच्या प्रत्युदाहरणात वगळण्याजोगा आकृतिबंध असूच शकत नाही, आणि A हे तर किमान स्वरूपाचे प्रत्युदाहरण आहे. अशी विसंगती निर्माण झाल्यामुळे सिद्ध होते की कोणत्याही प्रतल आलेखाचे शिरोबिंदू चार रंग वापरून उचित रीतीने रंगवता येतात.

हाइन्रिख हाइश
ही महत्त्वपूर्ण सिद्धता लक्षात ठेवून हाइन्रिख हाइश (Heinrich Heesch) या जर्मन गणितज्ञाने कित्येक वगळण्याजोगे आकृतिबंध शोधून काढण्याचा सपाटा लावला, अशा आशेने की ते सगळे आकृतिबंध मिळून एक अपरिहार्य संच बनावा. त्याने अंदाज केला की यासाठी निदान १०,००० वगळण्याजोगे आकृतिबंध मिळवावे लागतील. आकृतिबंधाच्या भोवतीच्या वलयातील शिरोबिंदूंची संख्या वाढवली की हे काम जास्त बिकट होई. बिरकॉफचा हिरा या आकृतिबंधाभोवती सहा शिरोबिंदूंचे वलय आहे. या सहा शिरोबिंदूंना चार रंग वापरून रंगवायचे ठरवले तर तत्त्वतः वेगळ्या (essentially different) अशा 31 रंगसंगती विचारात घ्यायला लागतात. जर वलयात दहा शिरोबिंदू असले तर हा आकडा 2461 होतो, आणि चौदा शिरोबिंदू असले तर 1,99,291 इतका अवाढव्य बनतो. चार रंगांच्या विधानाचा सोक्षमोक्ष लावण्यासाठी अठरा शिरोबिंदू असलेल्या वलयाचाही उपयोग करावा लागेल असे हाइशला वाटत होते. अशा कामासाठी संगणक वापरण्याखेरीज काही उपाय नव्हता. हाइशने संगणकाची मदत घेणे सुरू केले. पण तो काम करत असलेल्या जर्मनीमधील हॅनोवर विद्यापीठातील संगणक पुरेसे शक्तिमान नव्हते.
दुसरा पर्याय असा होता की प्रथम आकृतिबंधांचा, कदाचित मोठा थोरला, अपरिहार्य संच मिळवायचा व नंतर त्या संचातील प्रत्येक आकृतिबंध वगळण्याजोगा आहे याची खात्री करायची. हे प्रयत्न चालू असताना एक खळबळजनक घटना घडली. योशिओ शिमामोतो (Yoshio Shimamoto) या न्यू यॉर्कमधील ब्रुकहेवन लॅबोरेटरीत काम करणाऱ्या शास्त्रज्ञाने सप्टेंबर १९७१ मध्ये एक विशिष्ट आकृतिबंध शोधून काढला. त्या आकृतिबंधात चौदा शिरोबिंदूंनी बनलेल्या वलयाच्या अंतर्भागात 8 कोटीचा एक, 5 कोटीचे दोन आणि 6 कोटीचे पाच असे आठ शिरोबिंदू होते. याला शिमामोतोचा नाल (Shimamoto’s Horseshoe) असे म्हणतात. आकृती ७ मध्ये चौदा शिरोबिंदूंनी बनलेले वलय निळ्या रंगाने दाखवले आहे, आणि त्याच्या अंतर्भागातील आठ शिरोबिंदूंनी बनलेला आकृतिबंध तांबड्या रंगाने दाखवला आहे. (येथे वलय बनवणाऱ्या चौदा शिरोबिंदूंपासून निघणाऱ्या सर्व कडा दाखवलेल्या नाहीत.)
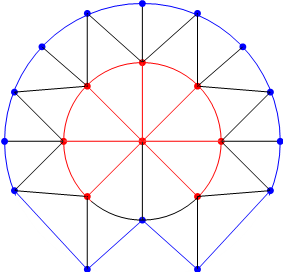
आकृती ७: शिमामोतोचा नाल
समजा चार रंगांचे विधान खरे नाही. शिमामोतोने दाखवले की जर वरील आकृतिबंध वगळण्याजोगा असेल तर तो एकातरी प्रत्युदाहरणात असला पाहिजे, व त्यामुळे विसंगती निर्माण होते. त्या काळातील प्रतिष्ठित आलेखशास्त्रज्ञ हॅस्लर व्हिटने (Hassler Whitney) आणि विल्यम ट्यूट (William Tutte) यांना शिमामोतोच्या युक्तिवादात काही चूक दिसली नाही. पण हा आकृतिबंध वगळण्याजोगा असणे आश्चर्यकारक ठरेल असे मात्र त्यांना वाटले. उलटपक्षी, हाइश व त्याचा एक विद्यार्थी यांनी तयार केलेले संगणक प्रायोजन (computer programming) हा आकृतिबंध वगळण्याजोगा आहे असा कल देत होते. निश्चिती व्हावी म्हणून शिमामोतोने नव्याने एक ताजे संगणक प्रायोजन करायला लावले. संगणकाने २६ तास कार्यवाही केल्यानंतर निर्वाळा दिला की शिमामोतोचा आकृतिबंध वगळण्याजोगा नाही! या निराशाजनक बातमीमुळे गाडी पुन्हा पहिल्या पदावर आली.
हाइन्रिख हाइशने जर्मनीतील हाम्बुर्ग व किएल येथील विद्यापीठांत वगळण्याजोग्या आकृतिबंधांच्या अपरिहार्य संचांबद्दल व्याख्याने दिली होती. वोल्फगांग हाकेन (Wolfgang Haken) हा तरुण विद्यार्थी १९४८ मध्ये हाइशने किएल येथे दिलेले व्याख्यान ऐकायला गेला होता. सुरवातीला हाकेनने गणिताच्या संस्थिती (topology) या विषयात काम केले. परंतु नंतर अमेरिकेतील अर्बाना-शॅम्पेन येथील इलिनॉय विद्यापीठात काम करू लागल्यावर त्याने आपले लक्ष चार रंगांच्या विधानाकडे वळवले. १९६९ साली हाइशने एखादा आकृतिबंधांचा संच हा अपरिहार्य संच आहे असे दाखवण्यासाठी एक विशिष्ट पद्धती शोधून काढली. कुठल्याही k कोटीच्या शिरोबिंदूला पहिल्यांदा 6 - k असा प्रभार (charge) नेमून द्यायचा, व नंतर हे प्रभार जरुरीप्रमाणे बदलत रहायचे, पण दरवेळी आलेखातील सर्व शिरोबिंदूंच्या प्रभारांची बेरीज मात्र बदलता कामा नये. या पद्धतीला हाकेनने विप्रभारण (discharging) असे नाव दिले. १९६७ पासून १९७१ पर्यंतच्या काळात हाइश आणि हाकेन यांनी एकमेकांच्या सहयोगाने बरेच काम केले. पण त्यानंतर त्यांच्या कामाच्या दिशा वेगळ्या झाल्या, इतक्या की हाइशने नव्याने शोधलेले वगळण्याजोगे आकृतिबंध गुप्तपणे स्वतःजवळच ठेवले.
१९७७ च्या जुलै महिन्यात एके दिवशी मुंबई विद्यापीठातील काम संपवून निर्मला घरी आली व चहा पिण्याआधीच ती मला म्हणाली, ‘चार रंग पुरतात’. मला प्रथम काहीच बोध झाला नाही, पण नंतर चहा पितापिता निर्मलाने जी कहाणी सांगितली ती मी ऐकत राहिलो. १९७३ साली वोल्फगांग हाकेनने इलिनॉय विद्यापीठाच्या तर्कशास्त्र चर्चासत्रात (logic seminar) वगळण्याजोग्या आकृतिबंधांच्या अपरिहार्य संचांबद्दल एक व्याख्यान दिले. असा संच शोधण्यासाठी त्या काळी उपलब्ध असलेल्या संगणकांपेक्षा जास्त सामर्थ्यवान संगणकांची जरूरी आहे असे प्रतिपादन हाकेनने केले. व्याख्यान संपल्यावर त्याच विद्यापीठातील प्राध्यापक केनेथ आपेल (Kenneth Appel) याने हाकेनला सांगितले की या प्रकल्पातील जे काम संगणकाशी संबंधित असेल ते लगेच हातात घ्यायला तो तयार आहे. हाकेनला फार हायसे वाटले, कारण त्याला संगणकक्षेत्रात काहीच गती नव्हती. आपेलला वेगवेगळ्या पंधरा यंत्र-भाषा (machine languages) अवगत होत्या. त्याने स्वतःच संगणकासाठी जरूर ते प्रायोजन तयार केले. याहीपेक्षा महत्त्वाची गोष्ट होती आपेलच्या मनाची उभारी. सुरुवातीला अवाढव्य वाटणारे काम दोन वर्षांच्या कालावधीत आटोक्यात येऊ लागले. त्या दोघांनी सुमारे 5000 आकृतिबंधांचा एक अपरिहार्य संच मिळवला, त्यातील आकृतिबंध संभवतः वगळण्याजोगे (likely to be reducible) होते. ते खरोखरच वगळण्याजोगे आहेत हे पडताळून पहाण्यास आपेलने गणनविधी (algorithms) लिहिले. इलिनॉय विद्यापीठातील IBM 360-168 या संगणकाला त्याच्या यादीतील प्रत्येक आकृतिबंध तपासण्यासाठी दोन-दोन तास लागत होते. सहा महिन्यानंतर आपेल व हाकेन यांनी या संचाची संख्या 5000 वरून 2000 च्या खाली आणली. तरीही हे काम संपायला आणखी दोन वर्षे लागावीत असा त्यांचा अंदाज होता. तेवढ्यात एक अनपेक्षित घटना घडली. १९७६ च्या उन्हाळ्यामध्ये इलिनॉय विद्यापीठात अतिशय सामर्थ्यवान अशा सायबर संगणकांची (Cyber computers) प्रतिष्ठापना करण्यात आली. ते वापरण्यासाठी आपेलने पहिला नंबर लावला, आणि आपले काम दोन महिन्यांत फत्ते केले.

आपेल आणि हाकेन आकृतिबंध न्याहाळताना
हे सगळे मला निर्मलाने पाच मिनिटात सांगितले खरे, पण आपेल व हाकेन अहोरात्र झगडत होते, संगणकाकडून आलेले प्रिंट-आउटस तपासत होते, संगणकाचे प्रायोजन सुधारत होते. सुरुवातीचे संगणक खूप मोठे असत, खोलीभर आकाराचे, आणि त्यांना कितीतरी इलेक्ट्रिकल तारा जोडलेल्या असत. प्रिंट-आउटवर एखादी अगदी टाकाऊ निष्पत्ती दृष्टीस आली तर आपेलला कळायचे की कुठली तरी तार संगणकातून निघून आली असली पाहिजे. तो मग ती तार नीट लावून घ्यायचा! आपेलला संगणक आपला सहकारी वाटू लागला होता, अर्थात वेगळ्या प्रकारचा मेंदू असलेला. त्यालाही समजून घेणे जरूर होते! सगळे मिळून जवळजवळ बाराशे तास संगणकाने कार्यवाही केली. आपेल व हाकेन या दोघांनी मिळून संभवतः वगळण्याजोग्या 1834 आकृतिबंधांचा एक अपरिहार्य संच शोधून काढला होता. मग या संचातील प्रत्येक आकृतिबंध खरोखरच वगळण्याजोगा आहे याची दोनदोनदा खात्री केली.
त्यानंतर एके दिवशी संध्याकाळी इलिनॉय विद्यापीठातील गणितविभागाच्या फळ्यावर ‘चार रंग पुरतात, फक्त काळजीपूर्वक फेरतपासणी करायचीय!’ असे खडूने लिहून आपेल व हाकेन घरी निघून गेले. दुसऱ्या दिवशी गणितविभागातील सर्वांच्या - प्राध्यापक, विद्यार्थी, सचिव, सेवक या सगळ्यांच्या - तोंडी हाच विषय होता. लवकरच ही बातमी जगातील अनेक गणितज्ञांपर्यंत पोचली. २३ जुलै १९७६ रोजी आपेल व हाकेन यांनी आपला एकशे चाळीस पानी शोधनिबंध ‘इलिनॉय जर्नल ऑफ मॅथेमॅटिक्स’ या नियतकालिकाकडे पाठवला. त्याबरोबरच अमेरिकन मॅथेमॅटिकल सोसायटीच्या बुलेटिनमध्ये व डिस्क्रीट मॅथेमॅटिक्स या नियतकालिकात त्यांनी निवेदने दिली. न्यू यॉर्क टाइम्समध्येही बातमी झळकली. तेव्हापासून अर्बाना (Urbana) येथील इलिनॉय विद्यापीठातील पोस्ट ऑफिसने पत्रांवर एक खास शिक्का मारायला सुरुवात केली. तो असा:

आपेल व हाकेन यांच्या कामगिरीबाबत संमिश्र प्रतिक्रिया झाल्या. त्यांनी दिलेल्या सिद्धतेत संगणकांचा वापर अनिवार्य होता. कुठल्याही महत्त्वपूर्ण गणिती विधानाबाबत असे प्रथमच घडत होते. सव्वाशे वर्षे भेडसावीत असलेला प्रश्न निकालात निघाल्याचे समाधान वाटत असले तरी जी सिद्धता आपण स्वतः पडताळून पाहू शकत नाही, ती मानायला बरेच शुद्ध गणित (Pure Mathematics) करणारे गणिती तयार होईनात. संगणकासाठी केलेले प्रायोजन कशावरून बिनचूक आहे, आपल्या नजरेआड संगणकांनी घेतलेले करोडो तार्किक निर्णय (logical decisions) का मानायचे अशा सवालांचे समाधानकारक जबाब मिळत नव्हते. उलटपक्षी, संगणकांचे प्रभुत्व दैनंदिन व्यवहारात आपण पूर्णपणे ग्राह्य धरत असताना त्यांच्या कार्यप्रणालीवर उगाच शिंतोडे उडवणे योग्य नाही, उच्च स्तरावरील गणितातही संगणकाला भूमिका बजावू दिली पाहिजे, सर्व गोष्टी मी स्वतःच तपासून बघेन असे आपण एरवीही म्हणत नाही मग इथेच का मोडता घालायचा अशी सकारात्मक बाजू मांडण्यात आली. गणितज्ञात सरळसरळ दोन गटच पडले. गणिती सिद्धता कशाला म्हणायचे याबद्दलच्या पूर्वापार चालत आलेल्या वादविवादाने पुन्हा उचल खाल्ली.
सरतेशेवटी मानवाच्या शारीरिक किंवा बौद्धिक शक्तीच्या बाहेरील बाबी हस्तगत करण्याचे संगणक हे एक साधन आहे हे मान्य करून गणितज्ञांनी आपेल व हाकेन यांच्या सिद्धतेला रडतखडत मान्यता दिली. त्यांचा शोधनिबंध सप्टेंबर १९७७ च्या ‘इलिनॉय जर्नल ऑफ मॅथेमॅटिक्स’ मध्ये प्रसिद्ध झाला. आपेल व हाकेन यांनी दिलेली सिद्धता हाइन्रिख हाइश याच्या मूलभूत कामावर आधारित होती, विशेषतः त्याने प्रस्तुत केलेल्या विप्रभारण या तंत्रावर. पण या दोघांच्या प्रयत्नांतून हाइशने अंग काढून घेतले असल्याने तो अंतिम यशाचा वाटेकरी ठरला नाही.
आपेल व हाकेन यांना व्याख्याने देण्यासाठी उत्तमोत्तम विद्यापीठांकडून आमंत्रणे येऊ लागली. गणितातील महत्त्वाच्या सिद्धता सामान्यपणे काही नव्या दिशा दर्शवतात. तसे त्यांच्या सिद्धतेने केलेले नाही ही वस्तुस्थिती आपेल व हाकेन मान्य करत. तरीही त्यांनी दिलेल्या सिद्धतेत एक नावीन्य होतेच. त्यामुळे त्यांचे भाषण ऐकायला गणित विभागातील सगळे लहानथोर उत्सुक असत. काही ठिकाणी मात्र त्यांच्या सिद्धतेचे कट्टर विरोधक होते. हे महाशय स्वतः तर भाषण ऐकायला जायचे नाहीतच, पण त्यांच्या मार्गदर्शनाखाली संशोधन करणाऱ्यांवर आपेल व हाकेन यांना भेटायची बंदी घालत, उगाच त्या तरुणांची मने असल्या थोतांडाने कलुषित व्हायला नकोत म्हणून!


आपेल आणि हाकेन
सर्वोच्च न्यायालयाने दिलेल्या एखाद्या महत्त्वपूर्ण निकालाचे पडसाद जसे दीर्घ काळ पडत राहतात आणि त्यावर गरमागरम चर्चा चालू रहाते, तसेच झाले आपेल व हाकेन यांच्या शोधनिबंधाचे. तो प्रसिद्ध होईपर्यंत त्यांचा 1834 आकृतिबंधांचा अपरिहार्य संच 1478 आकृतिबंधांवर आला होता. जवळजवळ वीस वर्षांनी १९९६ साली एन. रॉबर्टसन, डी. सँडर्स, पी. सीमोर आणि आर. थॉमस या चौघांनी अमेरिकन मॅथेमॅटिकल सोसायटीच्या Electronic Research Announcements मध्ये चार रंगांच्या प्रमेयाची वेगळी सिद्धता दिली. ती आपेल व हाकेन यांच्या सिद्धतेपेक्षा खूपच सोपी व सुटसुटीत होती. त्यांचा अपरिहार्य संच फक्त 633 वगळण्याजोग्या आकृतिबंधांचा होता, कोणताही प्रतल आलेख चार रंग वापरून उचित रीतीने रंगवण्यासाठी त्यांनी दिलेल्या गणनविधीला (algorithm) आपेल आणि हाकेन यांनी दिलेल्या गणनविधीच्या मानाने खूपच कमी वेळ लागत होता. शिवाय त्यांचे प्रायोजन औपचारिक संगणकीय भाषेत
होते, व म्हणून ते संगणकाला थोड्या मिनिटात वाचणे व तपासणे शक्य होते. (Formal language. अधिक माहितीसाठी इथे पाहा) पण ‘संगणकाचा वापर’ हा कळीचा मुद्दा तसाच होता. गणित ही सर्व शास्त्रांची राणी मानली जात असली तरी ती संगणकांची गुलाम झाली नाही म्हणजे मिळवली, असे उद्गार कानी पडत.
पण यापुढे जाऊन आपेल म्हणत असे की जर संगणक वापरायचे नाही असे ठरवले तर गणितज्ञ फक्त लहान सिद्धता असलेली प्रमेये सोडवण्यातच अडकून बसतील. असे म्हणण्याची जरुरी नव्हती, आणि ते रास्तही नव्हते. एखाद्या प्रमेयाची सिद्धता लहान आहे की मोठी आहे हा वेगळा प्रश्न आहे. सिद्धतेसाठी किती आकडेमोड करावी लागते यावर संगणकाचा उपयोग करणे अवलंबून राहू शकते. आपेल व हाकेन यांनी चार रंगांचे कोडे सोडवल्यानंतर वीस वर्षांच्या आत अँड्रयू वाइल्स (Andrew Wiles) या गणितज्ञाने फर्माने घातलेल्या प्रसिद्ध कोड्याची एक गहन व विस्तृत सिद्धता दिली. तिच्यात संगणक वापरण्याचा प्रश्नच उद्भवत नव्हता. त्या कोड्याचा पुढे कधीतरी विचार करू.
आपेल व हाकेन या गणितज्ञांचे मूळचे संशोधनविषय बीजगणित (algebra) व संस्थिति (topology) असे होते. आलेखशास्त्राच्या नव्या प्रांतात शिरून त्यांनी केलेली कामगिरी निश्चितच अभिनंदनीय होती. संगणकाचा उपयोग करण्याची त्यांना हौस नव्हती, ती त्यांची गरज ठरली. आपल्या प्राथमिक यशामुळे त्यांनी संगणकाला गणिती प्रक्रियांमध्ये एक विशिष्ट स्थान (niche) प्राप्त करून दिले. आधी न सुटलेली प्रमेये संगणकाचा वापर करून सोडवण्याचे प्रयत्न होऊ लागले. त्यांपैकी एकाचा आवर्जून उल्लेख करता येईल. समचयशास्त्र (Combinatorics) या गणिताच्या भागात दहा कोटिकेचे प्रक्षेप प्रतल (projective plane of order ten) अस्तित्वात असते की नाही याचा निर्णय कित्येक दशके लागत नव्हता. अशा प्रक्षेप प्रतलात 102 + 10 + 1 = 111 बिंदू असावे लागतात. क्लेमेंट लॅम (Clement Lam) या गणितज्ञाने व त्याच्या दोन सहसंशोधकांनी १९८६ पर्यंत गणिती युक्तिवादांनी असे प्रतल अस्तित्वात असू शकत नाही हे जवळजवळ सिद्ध केले होते, पण त्या सिद्धतेची एक पायरी बाकी होती. शेवटी १९८९ मध्ये CRAY-1A या महासंगणकाला (supercomputer) तीन महिने कामाला लावून त्या तिघांनी ती सिद्धता पूर्ण केली.
अशा तात्त्विक प्रमेयांखेरीज व्यावहारिक गणितातही संगणकांचा सर्रास उपयोग होऊ लागला. गूढलेखनशास्त्रात (cryptography) अतिशय मोठ्या संख्यांचे अवयव मिळवता आले तर फायद्याचे असते. संगणकाच्या मदतीने वीस-वीस अंकी संख्यांचे अवयव काही सेकंदात मिळू लागले. संगणकाची स्मृती आणि गती मानवी मेंदूपेक्षा सरस असू शकते ही गोष्ट गॅरी कास्पारॉव्ह या जगज्जेत्या बुद्धिबळपटूला जेव्हा डीप ब्ल्यू या संगणकाने १९९७ मध्ये हरवले तेव्हा उघड झाली. प्रचंड आकडेमोड करावी लागत असेल, तर ती फक्त कागद-पेन्सिलीच्या साह्याने शक्य होत नाही, तिच्यासाठी संगणकाची मदत घेणे योग्यच आहे हे आता सर्वमान्य झाले आहे.
फक्त जलद गतीने मोठमोठी आकडेमोड करण्यासाठीच नाही तर गणिती तर्काने एखाद्या प्रमेयाची सिद्धता मिळवून देण्यासाठीही संगणक सज्ज होत आहेत. मानवानेच लिहिलेली एक संगणकप्रणाली (computer software) ‘सिद्धतेचा सहकारी’ (proof assistant) म्हणून उपयोगी पडत आहे. २००४ सालच्या सप्टेंबर महिन्यात कॅनेडियन संगणकशास्त्रज्ञ जॉर्ज गोंथिये (Georges Gonthier) याने पूर्णतः यांत्रिक रीतीने तपासलेली (fully machine-checked) चार रंगांच्या प्रमेयाची सिद्धता पुरवली. यासाठी त्याने Coq नावाचा सिद्धतेचा सहकारी वापरून १९९६ मध्ये रॉबर्टसन आदींनी प्रस्तुत केलेली या प्रमेयाची सिद्धता औपचारिक भाषेत (formal language) कार्यान्वित केली, व त्यामुळे अनेक जणांमध्ये वास करणाऱ्या संशयाच्या पिशाच्चाला पिटाळून लावले. या सगळ्या घडामोडींना आपेल व हाकेन यांनी संगणकाच्या साह्याने दिलेली सिद्धता कारणीभूत ठरली.
२००६ साली मुंबई विद्यापीठातून निवृत्त होईपर्यंत निर्मलाने बऱ्याच वेळा आलेखशास्त्र हा विषय शिकवला. ती विद्यार्थ्यांना सांगायची, “नकाशातील शेजारच्या प्रदेशांना वेगळे रंग द्यायचे ठरवले तर चारच रंग पुरतात असे सिद्ध झाले आहे; पण आपण वर्गात पाच रंग कसे पुरतात एवढेच सिद्ध करणार आहोत. त्यानंतर चार रंग पुरे पडतात हे कोणी व कसे सिद्ध केले याची कल्पना देता येईल. रॉबिन विल्सन यांचे ‘चार रंग पुरतात’ (Robin Wilson’s ‘Four Colors Suffice’) हे पुस्तक खूप माहितीपूर्ण व मनोरंजक आहे. ते स्वतः गणितज्ञ आहेत, त्यांनी आपल्या विभागाला दोन-तीनदा भेट दिली आहे, ते उत्तम व्याख्यातेही आहेत. पण शेवटी ‘संगणकाय तस्मै नमः’ असेच म्हटले पाहिजे.”

रॉबिन विल्सन आणि प्राध्यापक श्रीखंडे, मुंबई विद्यापीठात

रॉबिन विल्सन यांचे पुस्तक
(पुढील भाग इथे)
---
बालमोहन लिमये
(balmohan.limaye@gmail.com)

लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.
बालमोहन लिमये यांचे इतर लिखाण


प्रतिक्रिया
प्रदीर्घ लेख आवडला.
संगणकाचे काम तपासता येत नसेल तर ग्राह्य धरायचे का हा प्रश्न खरंच सतावणारा आहे.
सुंदर लेख. वगळण्याजोग्या
सुंदर लेख. वगळण्याजोग्या आकृतिबंधांचा अपरिहार्य संच मिळविणे ही संकल्पना समजली, पण शिमामोतोचा नाल हा एकच आकृतिबंध वगळण्याजोगा ठरला असता तर चार रंगांच्या अनुमानाची सिध्दता शक्य झाली असती ह्याचे स्पष्टीकरण झाले नाही असे वाटते. हा नाल अशा कुठल्या अपरिहार्य संचाचा भाग होता का की ज्यातला दुसरा कुठलाही आकृतिबंध वगळण्याजोगा होता?
स्पष्टीकरण
तुम्हाला पडलेला प्रश्न बरोबर आहे. लेखात काही स्पष्टीकरणाची भर घातली आहे, ती पहावी. शिमामोतोने त्याच्या नालासंबंधी शोधनिबंध लिहिला नाही; निदान `मॅथेमॅटिकल रिव्ह्यूज'मध्ये काही आढळत नाही. व्हिटने आणि ट्यूट यांनी १९७२ साली लिहिलेल्या एका शोधनिबंधात शिमामोतोच्या युक्तिवादाचा उल्लेख आहे.
आता मला पडलेला एक प्रश्न. विचित्रबुद्धी हे टोपणनाव कुणी का घ्यावे?
धन्यवाद
स्पष्टीकरणाबद्दल धन्यवाद. एका तरी प्रत्युदाहरणात हा नाल एक आकृतिबंध म्हणून असला पाहिजे ह्याविषयीचा युक्तिवाद मला अर्थातच माहीत नाही.
Niche
'Niche' करता "विशिष्ट जागा" ऐवजी "विशिष्ट स्थान" किंवा "खास जागा" हे शब्दसमूह विचित्रबुध्दीच्या कानांना अधिक भावतात.
सजातीय
मान्य! सजातीय शब्द एकत्र आलेले बरे.
कडबोळं
> नकाशा रंगवण्यासाठी पाच रंग पुरतात हे आपण मागील भागात पाहिले. पण चारच रंग पुरू शकतात यासाठी लागणारा युक्तिवाद जाणून घेण्याचे कुतूहल असणे साहजिक आहे.
ह्या प्रकरणाला एक गंमतीदार आणि अनपेक्षित उपकथानक आहे. गणितात सर्वसाधारण चित्र असं दिसतं की कोणत्याही संकल्पनेच्या अनुषंगाने काही सैद्धान्तिक प्रश्न उद्भवतात. जसजशी ही संकल्पना जास्त गुंतागुंतीची होत जाते तसतसे हे प्रश्नही अवघड होत जातात. उदाहरणार्थ, द्विमितीय भूमितीपेक्षा त्रिमितीय भूमिती जास्त अवघड असते, आणि तशी ती असणार याचं कुणालाही आश्चर्य वाटत नाही. किंवा उदाहरणार्थ, दुसऱ्या कोटीच्या बहुपदीचं मूळ काढणं सोपं आहे. तिसऱ्या कोटीसाठी हे जास्त अवघड आहे आणि चौथीसाठी खूपच अवघड आहे. हेही असं असणार याचं कुणाला आश्चर्य वाटत नाही.
पण इथे बाब वेगळी आहे. पृथ्विगोलावर काढलेला कुठलाही नकाशा चार रंगांत रंगवता येतो ह्या प्रमेयाची विस्तृत चर्चा वर आलीच आहे. ह्याची सिद्धता भयंकर किचकट आहे इतकं उघड आहे. पण समजा आपण पृथ्विगोलाऐवजी कडबोळ्याच्या पृष्ठभागासाठी हाच प्रश्न विचारला. आता कडबोळं हे गोलापेक्षा जास्त गुंतागुंतीचं (किंवा खरं तर आडनिडं) असल्यामुळे हा प्रश्न जास्त अवघड होईल असं वाटणं साहजिक आहे. पण तसं नाही. कडबोळ्यासाठी ही रंगांची कमाल संख्या चारऐवजी सात आहे, पण इतकंच नव्हे तर या प्रमेयाची सिद्धता शंभरपटींनी सोपी आहे. कडबोळ्यासाठीचा प्रश्न गोलाच्या कित्येक दशकं आधी सुटला होता.
टीप: मला ‘ऐसी’वर तळटीपा देता येत नाहीत आणि कशा द्यायच्या हे शिकण्याची थोडीही इच्छा नाही. पण ‘कडबोळं’ याचा तांत्रिक गणिती अर्थ ‘compact orientable 2-manifold of genus one’ असा आहे.
- जयदीप चिपलकट्टी
(होमपेज)
Torus
कडबोळं या शब्दाने Torus ची चांगली कल्पना येते. त्याला surface of a donut असेही संबोधतात. त्याऐवजी आपण मेदूवड्याचा पृष्ठभाग असे म्हणू शकतो.
कडबोळं
कडबोळं ह्याला torus न म्हणता solid torus म्हटले पाहिजे. मेदूवड्याचा पृष्ठभाग हे torus चे वर्णन यथार्थ आहे.
कडबोळ्याचा पृष्ठभाग = torus
कडबोळ्याचा पृष्ठभाग = torus हेही बरोबर आहे.
.
हा लेखही अभ्यास करायला लावणारा आहे (निदान मला तरी). पण आपल्याला कुणी परीक्षेला बसवणार नाही हे माहिती असताना केलेला अभ्यास सुसह्य असतो.
या लेखांमधून एकेका प्रमेयाचं chronological documentation होतंय ते वाचायला मजा येते आहे.
लेखमाला उत्कृष्ट पद्धतीने
लेखमाला उत्कृष्ट पद्धतीने सुरू आहे. बऱ्याच तांत्रिक गोष्टी डोक्यावरून जात आहेत, अर्थात हा दोष माझ्यासारख्यांच्या आकलनशक्तीचा.
माणिक टेंबे यांचा अभिप्राय
गणिताच्या निमित्ताने या लेखाचा सहावा भाग मला खूपच आवडला. नकाशा रंगवायला पाच रंग पुरेसे असतात हे प्रमेय मी शिकले होते. चार रंग पुरेसे असतात याची सिद्धता जेंव्हा संगणक वापरून दिली गेली तेंव्हा अशी सिद्धता मान्य करावी की न करावी यासंबंधी उठलेला वादंगही मला ठाऊक होता पण या दोन सिद्धतांच्या मधल्या पायऱ्या या लेखात मी प्रथमच वाचल्या आणि समजून घेतल्या. एका महान प्रमेयाकडे जाणाऱ्या या वाटा समजून घेणे हे खरच खूप आनंद देऊन गेले. फर्माच्या शेवटच्या प्रमेयावर Simon Singh यांनी Fermat’s Last Theorem (किंवा Fermat’s Enigma) नावाचे पुस्तक लिहिले आहे, ते वाचताना जो गणिती आनंद मिळालेला तसाच आनंद चार रंगांच्या समस्येचा हा लेख वाचून मिळाला.
इतिहास घडवणाऱ्या या गणिती प्रमेयांच्या कहाण्या अधिकाधिक लोकांपर्यंत पोचल्या पाहिजेत आणि मराठी भाषेत हे सर्व आले पाहिजे.
माणिक टेंबे
महासंगणक
Supercomputer ला मराठीत “अतिविशाल संगणक” नव्हे, तर “महासंगणक” ह्मणावयास हवे. इंग्रजीतील super या विशेषणाचा अर्थ “ of the highest degree, power, etc.” असा होतो.
….शेवटी मदांध तख्त फोडते मराठी!
मान्य!
बदल केला आहे.