गणिताच्या निमित्ताने - भाग १
गणिताच्या निमित्ताने - भाग १
बालमोहन लिमये
(प्रा. बालमोहन लिमये यांच्या लेखमालेचा हा पहिला भाग आहे. गणिताशी संबंध आल्यामुळे त्यांच्या आयुष्याच्या वेगवेगळ्या काळात अवतरलेल्या अनेकविध गोष्टींची ओळख या लेखमालेतून प्रा. लिमये वाचकांना करून देतील. त्यात गणिताच्या निमित्ताने त्यांना भेटलेल्या काही खास व्यक्ती असतील तसेच त्यांच्या या दीर्घ प्रवासात लागलेली काही स्थळेही असतील. वाचकाला त्यातून गणिताविषयी आणि गणितींविषयीही रोचक, रंजक आणि उद्बोधक गोष्टी समजतील, आणि त्यातून वाचकांचे गणिताशी काही प्रमाणात मैत्र जुळायला मदत होईल. - ऐसी अक्षरे)
माझ्या नेहमीच्या दंतवैद्यांचा दवाखाना माझ्या राहत्या घरापासून खूप लांब होता. म्हणून कोविद-१९ची सार्वजनिक साथ (pandemic) चालू झाल्यावर मी जवळच्या एका दंतवैद्यांकडे गेलो. दात तपासून झाल्यावर डॉ. प्रणोती प्रधान यांनी मला सहज विचारले की मी काय काम करायचो. मी आय. आय. टी.मध्ये प्राध्यापक होतो हे सांगितल्यावर त्या उद्गारल्या ‘अरे वा!’ मग त्यांनी विचारले माझा विषय कोणता. मी म्हटले ‘गणित’. तत्क्षणी त्यांच्या तोंडून ‘अरे बापरे’ असे उद्गार निघाले. आय. आय. टी.साठी ‘अरे वा!’ आणि गणितासाठी ‘अरे बापरे’ या भिन्न प्रतिक्रिया मी अनेक वेळा अनुभवल्या आहेत, विशेषत: वैद्यकीय पेशातील किंवा कला विभागातील लोकांबरोबर बोलताना. याचे कारण या लोकांना आमच्या संस्थेबद्दल कुतुहलमिश्र आदर असतो, पण त्यांनी गणिताबद्दल एक प्रकारचा बाऊ करुन घेतलेला असतो. त्याची कारणे अनेक असू शकतात. प्राथमिक शाळेपासून गणित घोकंपट्टीसारखे शिकवले जाणे हे एक महत्त्वाचे कारण. नंतर माध्यमिक शाळा सोडल्यावर शास्त्रशाखेऐवजी कलाशाखेकडे वळल्यावर, आणि शास्त्रशाखेतही गणिताऐवजी जीवशास्त्र विषय निवडल्यावर ‘एकदाची गणिताची ब्याद संपली’ म्हणून बरेच जण एक सुस्कारा टाकतात. एखाद्या प्रश्नात गणिताचा थोडा जरी संबंध येत असला, तर तिकडे ढुंकूनही बघत नाहीत. मग गणिताचा कायम दुरावा वाटायला लागतो. एका उत्तम महाविद्यालयाच्या प्राचार्यांचा विषय होता इंग्लिश. पण त्यांना बऱ्याच वेळा असे स्वप्न पडायचे की ते गणिताच्या परीक्षेत वारंवार नापास होत आहेत आणि म्हणून त्यांना प्राचार्यपद सोडावे लागणार आहे. गणिताची भीति मनात किती खोलवर घर करून राहते, नाही?
मी या लेखमालेत ज्यांना गणिताविषयी आवड आहे ती वाढीला लावायचा आणि ज्यांना गणिताबद्दल काहीशी भीति आहे ती थोडी तरी कमी करायचा प्रयत्न करणार आहे. प्रत्यक्ष गणिताचा भाग थोड्याच ठिकाणी आला असला तरी मी शाळेत गणित शिकायला लागल्यापासून गणिताचा प्राध्यापक म्हणून आय. आय. टी.मधून निवृत्त होईपर्यंत, आणि नंतरही, गणिताच्या निमित्ताने माझा काही विशेष व्यक्तींशी संबध आला, काही खास प्रसंगांतून मी गेलो, त्याबद्दल लिहिणार आहे. माझ्या गणिती प्रवासात लागलेली काही स्थळे, तिथली दृश्ये आणि संवाद यांचा उल्लेख करणार आहे. यातल्या काही गोष्टींचा गणिताशी फार लांबचा संबंध असू शकतो, त्याला बादरायण संबंध म्हणा पाहिजे तर, पण गणिताच्या धाग्यात त्या सगळ्या गुंफता येतात. जसे श्रीकृष्णाने अर्जुनाला ‘निमित्तमात्रं भव सव्यसाचिन्’ असे सांगितले, त्याप्रमाणे, येथे गणित हे निमित्तमात्र आहे. जाता जाता गणित ही काय चीज आहे, गणिती माणसे कशाकशाचा व कशा प्रकारे विचार करतात याबद्दलही सांगता येईल. त्याने गणित कशाशी खातात याची अंधुकशी कल्पना जरी आली तरी पुरे. मात्र दर वेळी गणितातील या प्रमेयाचा उपयोग काय ते सांगा असे घोषवाक्य मनात आणले नाही तर बरे होईल, कारण बऱ्याचदा ती प्रमेये फक्त एक स्वाभाविक कुतूहल शमवण्याच्या प्रयत्नातून निर्माण झाली असतात; त्यांचा काही तरी उपयोग झालाच पाहिजे अशी अपेक्षा ठेवणे वाजवी नाही.
शाळा आणि कॉलेज
शिक्षण प्रसारक मंडळीने पुण्यात चालवलेल्या नूतन मराठी विद्यालय या प्रशाळेत शिकत असताना मी गणिताकडे एक खूप गुण मिळवून देणारा विषय़ या दृष्टीने बघत असे. मला प्रावीण्य मिळवायचे होते संस्कृतमध्ये, माझ्या वडिलांसारखे. आमच्या शाळेत शालांत परीक्षेसाठी ‘लोअर मॅथेमॅटिक्स’ किंवा ‘हायर मॅथेमॅटिक्स’ यापैकी एक विषय घ्यावा लागे. ओघानेच आले की मी ‘लोअर मॅथेमॅटिक्स’ पत्करले, आणि शिवाय अंकगणित हा ऐच्छिक विषय घेतला. दोन्ही विषयात मला भरपूर गुण मिळाले खरे, पण पैकीच्या पैकी मात्र नाही मिळाले. त्या काळात शालांत परीक्षेत उत्तम गुण मिळाले तर कॉलेजमध्ये शास्त्रशाखेत प्रवेश घ्यायचा, आणि दोन वर्षांनी प्रिप्रोफेशनल (Preprofessional) किंवा इंटर सायन्स (Inter Science) या परीक्षेनंतर इंजिनिअरींग किंवा मेडिकल कॉलेजमध्ये प्रवेश मिळवायचा असा पायंडाच पडलेला होता. पुण्यामुंबईत शालांत परीक्षा घेत असे माध्यमिक शाळा प्रमाणपत्र परीक्षामंडळ (Secondary School Certificate Examination Board). 1960 सालापर्यंत मुंबई राज्याचे (Bombay State) एकच मंडळ होते. त्यानंतर महाराष्ट्र आणि गुजराथ यांची वेगळी मंडळे झाली. त्या सालच्या शालांत परीक्षेत अनिल खर्शीकर, मी आणि भालचंद्र फडके हे तीन मित्र पहिल्या तीन नंबरात आले, व तिघांनीही बी. ए. ही पदवी मिळवण्यासाठी कला शाखेत प्रवेश घेतला. तेव्हा आम्हा तिघांच्या सामाईक मित्रांना साहजिकच आश्चर्य वाटले. अर्थात् आम्हा तिघांची कारणे वेगवेगळी होती. एक नमूद करण्यासारखी गोष्ट म्हणजे गणित (Mathematics) व सांख्यिकी (Statistics) हे विषय कला आणि शास्त्र अशा दोन्ही शाखांत अभ्यासता येत असत. पुणे आणि मुंबई येथील विद्यापीठांत ते अजूनही शक्य आहे. बहुधा असे हे दोनच विषय असावेत.
मी शि. प्र. मंडळीच्याच स. प. महाविद्यालयात प्रवेश घेतला, आणि गणित व संस्कृत असे दोन्ही विषय पहिली तीन वर्षे सारख्या प्रमाणात अभ्यासले. स. प. महाविद्यालयात १९३३ पासून गणित शिकवणारे निष्णात व नामवंत प्राध्यापक दत्तात्रय वामन केरकर नुकतेच, म्हणजे जानेवारी १९६० मध्ये निवृत्त झाले होते. संस्थेच्या विनंतीला मान देऊन त्यांनी अध्यापनाचे काम चालू ठेवले असले तरी ते फक्त बी. ए. आणि बी. एस्सी.च्या तिसऱ्या व चौथ्या वर्षांतील मुलांना शिकवत. दोनएक वर्षांनी त्यांनी हे शिकवणेही थांबवले. म्हणून मी कॉलेजजवळच्या त्यांच्या बंगल्यावर जाऊन खाजगीरीत्या शिकत असे, आठवड्यांतून दोनदा. प्रा. केरकर इंग्लंडमधील केंब्रिज विद्यापीठातून रॅंग्लर झाले होते. नंतर त्यांनी भारतीय प्रशासन सेवेत (I.A.S.) प्रवेश मिळवला होता, पण काही कारणाने ती नोकरी सोडून ते स. प. महाविद्यालयात शिकवू लागले. त्यांना सिगरेट ओढल्याशिवाय राहवत नसे. वर्गात शिकवतानाही सिगरेट ओढण्याची खास परवानगी त्यांना होती. आख्यायिका अशी होती की शिकवत असताना ते एका हातात खडू व दुसऱ्या हातात सिगरेट धरत. मग फळ्यावर लिहिलेले पुसण्यासाठी हातात डस्टर कसा घेता येणार? त्यासाठी त्यांनी आपल्या पुढच्या दातांपैकी एक दात काढून घेतला होता, व बरोब्बर त्या जागी ते सिगरेट ठेऊन देत!

प्राध्यापक द. वा. केरकर व सौ. सुमित्राबाई केरकर, १९६०
प्राध्यापक केरकरांच्या पत्नी सुमित्राबाई यांची सामाजिक बांधिलकी सर्वश्रुत होती. विशेषतः विद्यार्थी साहाय्यक समितीच्या त्या निष्ठावंत कार्यकर्त्या होत्या. मी प्रा. केरकरांच्या घरी जाई तेव्हा सुमित्राबाई अनेक विद्यार्थिनींची सोय लावून देण्यात मग्न असत.
प्राध्यापक केरकरांशिवाय गणित शिकवणाऱ्यात होत्या डॉ. मधुमालती आपटे. त्यांनी फ्रान्सला जाऊन पीएच. डी. पदवी मिळवली होती. पण १९६१ सालच्या जुलै महिन्यापासून त्या फर्ग्युसन कॉलेजमध्ये निघून गेल्या. त्या खेरीज प्राध्यापक मनोहर राइलकर यांनी १९५४ साली मुंबई विद्यापीठातून सांख्यिकी या विषयात एम्. एस्सी. ही पदवी आणि १९५९ साली पुणे विद्यापीठातून गणित या विषयात एम. ए. ही पदवी मिळवली होती. ते मुख्यतः सांख्यिकीचे, पण गणिताचेसुद्धा काही कोर्सेस शिकवत. दुर्दैवाने माझ्या कॉलेजमधील पहिल्या तीन वर्षांत आमच्या वर्गाला केरकर, आपटे, राइलकर या तिघांपैकी कुणीच एकही कोर्स शिकवला नाही. नव्याने रुजू झालेले इतर प्राध्यापक सगळे कोर्सेस शिकवून गेले.
कॉलेजच्या पहिल्या वर्षी मी देवधर गणित संस्थेत (Devadhar Mathematics Institute) शिकायला जात असे. विश्वनाथ कृष्ण देवधर हे आधी पेरुगेटजवळच्या भावे हायस्कूलमध्ये शिक्षक होते. नुकतेच त्यांनी क्लासेस काढले होते. सरांचे शिकवणे मला खूप पद्धतशीर व नीटनेटके वाटत असे. मात्र त्यांनी विचारलेले भूमितीतले प्रश्न किंवा उपप्रमेये (riders) सोडवणे मला कठीण जायचे. त्यांची शिकवण्याची पद्धत खास होती. एके दिवशी वर्गात आल्यावर त्यांनी विचारले की 1 ते 100 पर्यंतच्या सगळ्या आकड्यांची बेरीज किती होते. थोडा वेळ मुलांना बेरजा करू दिल्यावर ते म्हणाले की शंभरपर्यंत पोचायला बराच वेळ लागेल नाही का, आणि मध्येच एखादी चूक झाली तर पुढच्या सगळ्याच बेरजा चुकणार; अशा बेरजा करत राहायला तुम्ही काही पहिली-दुसरीतले विद्यार्थी नाहीत. त्यांनी सांगितले की पहिल्या काही बेरजांकडे नीट पाहून त्यांतून काही आराखडा (pattern) दिसतो आहे का ते बघा. कुणालाच काही विशेष दिसत नव्हते. मग त्यांनी एक सूचना (hint) केली: येणाऱ्या बेरजेला दोनने गुणा व मग ती संख्या कोणत्या दोन संख्यांचा गुणाकार करून मिळते याचा विचार करा. आमच्या बॅचमध्ये सुभाष फाटक नावाचा एक हुशार मुलगा होता. सरांची सूचना ऐकताच त्याने लगेच वहीत कोष्टक लिहिले :
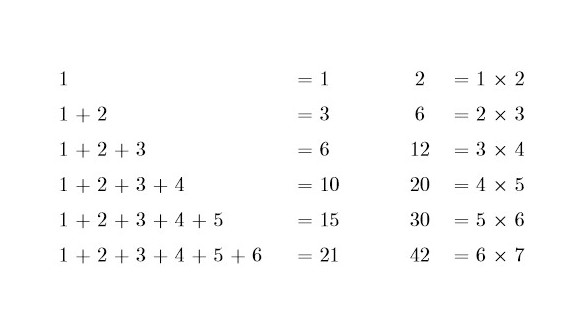
सुभाष म्हणाला की असेच जर पुढे होत गेले तर 2(1 + 2 + ... + 99 + 100) = 100 × 101 = 10100, आणि म्हणून 1 ते 100 पर्यंतच्या सगळ्या आकड्यांची बेरीज 10100/2 = 5050 होईल! देवधर सर बेहद्द खूष झाले. सुभाषची निरीक्षणशक्ती आणि कल्पनाशक्ती कमालीची होती. सर तेवढ्यावर थांबले नाहीत. त्यांनी फळ्यावर लिहिले ‘n हा कोणताही आकडा दिला असेल तर 1 ते n पर्यंतच्या सगळ्या आकड्यांची बेरीज n × (n + 1)/2 इतकी होते.’ पण ते म्हणाले ‘हा आपला कयास आहे. त्याची खातरजमा करण्यासाठी आपण प्रत्येक वेळी एक आकडा मिळवून बेरीज आपल्या उत्तराइतकी आहे ना असे बघत बसलो तर ते कधीच संपणार नाही, कारण आकडे अनंत आहेत. यासाठी फळ्यावर लिहिलेल्या विधानाची सिद्धता द्यावी लागेल. ती कशी द्यायची ते मी आज शिकवणार आहे.’
त्या दिवशी देवधर सरांनी वर्गाला गणिती विगमन (mathematical induction) कसे करतात ते समजावले. एखादे विधान प्रत्येक आकड्यासाठी सिद्ध करायचे असेल तर ते प्रथम n = 1 या सुरुवातीच्या आकड्यासाठी खरे आहे हे पडताळून बघायचे. याला मूळ बाब (base case) असे म्हणतात. नंतर k हा कुठलाही आकडा असेल तर ते विधान n = k साठी गृहीत धरायचे आणि n = k + 1 साठी सिद्ध करायचा प्रयत्न करायचा. याला विगमन पायरी (inductive step) असे म्हणतात. या प्रयत्नात जर आपण यशस्वी झालो तर आपले विधान प्रत्येक आकड्यासाठी सिद्ध होते, कारण k हा कुठलाही आकडा असेल तर आपण 1 पासून सुरुवात करून क्रमाक्रमाने k पर्यंत पोचू शकतो. अनंत गोष्टी पडताळून पाहाव्या लागू नयेत म्हणून गणितज्ञांनी काढलेली ही एक क्लृप्ती आहे.
प्रस्तुत विधान आहे : 1 + 2 + ... + (n - 1) + n = n × (n + 1)/2. जर n = 1 असेल तर समीकरणाच्या दोन्ही बाजू समान आहेत, 1 च्या बरोबर. म्हणजे मूळ बाब तर ठीक आहे. आता विगमन पायरीकडे जाऊ. k हा कुठलाही आकडा असेल तर हे विधान n = k साठी गृहीत धरू या, म्हणजे 1 + 2 + ...+ (k - 1) + k = k × (k + 1)/2 असे मानू या. मग
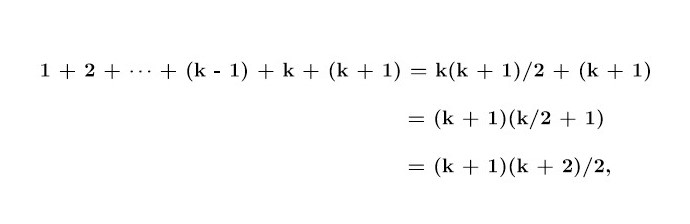
याचा अर्थ आपण दिलेले विधान n = k + 1 साठी सिद्ध करू शकलो! या प्रकारे आपल्याला छातीठोकपणे प्रस्तुत विधान प्रत्येक आकड्यासाठी खरे आहे असे म्हणता येते.
उदाहरणार्थ, k = 100 घेऊ या, व प्रत्यक्ष बेरीज न करता 1 + 2 + ... + 99 + 100 = 100(100 + 1)/2, असे मानू या. मग
1 + 2 + ... + 99 + 100 + 101 = 100(100 + 1)/2 + 101 = (100 + 1)(100 + 2)/2,
म्हणजे आपले विधान k + 1 = 101 साठी सिद्ध झाले.
क्लासमध्ये फारच महत्त्वाची अशी गणिती विगमन पद्धती आम्ही शिकलो होतो. सरांनी सांगितले की एखादे विधान पहिल्या काही आकड्यांसाठी खरे असले तरी ते प्रत्येक आकड्यासाठी खरे असेलच असे नाही. त्यांनी चटकन उदाहरण दिले. समजा आपले विधान आहे ‘n हा कोणताही आकडा दिला असेल तर 1 ते n पर्यंतच्या सगळ्या आकड्यांचा गुणाकार n या आकड्याच्या घनापेक्षा कमी असतो’, म्हणजे 1 × 2 × ... × (n-1) × n < n3, असे. हे विधान n = 1, 2, 3, 4, 5 आकड्यांसाठी खरे आहे. पण n = 6 साठी ते खरे नाही, कारण पहिल्या सहा आकड्यांचा गुणाकार 720 होतो, पण सहाचा घन 216 आहे. त्यामुळे वर वर बघून ठोकून दिले तर चालत नाही.
पुढच्या वेळी आम्ही क्लासला आलो तेव्हा देवधर सरांनी फळ्यावर खालीलप्रमाणे लिहून ठेवले होते.
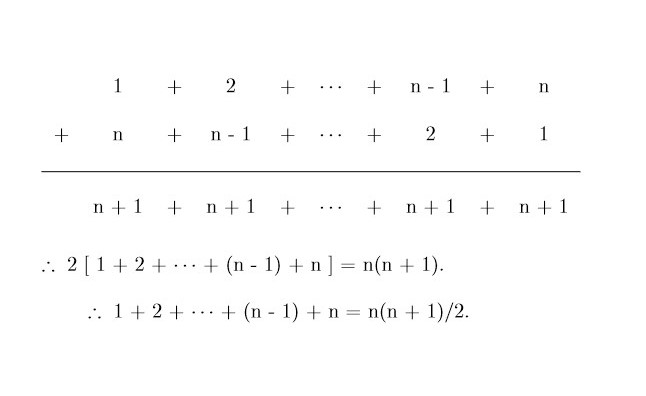
आदल्या तासाला सरांनी समजावून दिलेल्या उत्तरापेक्षा हे उत्तर किती सुटसुटीत व सहज कळण्यासारखे होते! ऐकिवात आहे की लोकमान्य टिळक शाळेत असताना त्यांनी असेच उत्तर दिले होते! सर म्हणाले की त्यांनी हे उत्तर काल सांगितले नाही, कारण गणिती विगमन पद्धती समजावून सांगणे हा त्यांचा मुख्य उद्देश होता. ती पद्धती आम्हाला खूप ठिकाणी उपयोगी पडणार होती. आज फळ्यावर लिहिलेले उत्तर त्यांनी प्रथमच सांगून टाकले असते तर आम्ही कोणी गणिती विगमनाकडे फारसे लक्ष दिले नसते. क्लास संपताना सरांनी गृहपाठ दिलाच : 1 ते n पर्यंतच्या सगळ्या आकड्यांच्या वर्गांची बेरीज किती होते ते सांगा व तसे सिद्ध करा.
कॉलेजच्या चौथ्या वर्षात गणित निवडायचे की संस्कृत हा निर्णय घेणे मला खूप जड गेले. संस्कृतप्रमाणे मला गणितही आवडू लागले होते. प्रथम देवधर सरांच्या शिकवण्याच्या पद्धतीमुळे आणि नंतर प्रा. केरकर यांच्या शिकवणीमुळे आपला गणितात टिकाव लागेल असा विश्वास वाटू लागला होता. शेवटी मी गणित हाच विषय निवडला याला एक कारण असे होते की व्यवसाय म्हणून गणित निवडले तरी छंद म्हणून संस्कृतशी सहज संपर्क ठेवता येईल, पण व्यवसाय म्हणून संस्कृत निवडले तर गणिताशी संपर्क ठेवणे फार कठीण गेले असते. गणित घेण्याचा निर्णय झाला खरा, पण आधीच्या तीन वर्षात मी स. प. महाविद्यालयात शिकलेले गणिताचे कोर्सेस यथातथाच होते. त्या काळात पुण्यातील दुसरे उत्तम कॉलेज म्हणजे फर्ग्युसन कॉलेज. माझे वडील याच कॉलेजात १९१७ ते १९२० या काळात शिकले होते. त्यांचा संस्कृत हा मुख्य विषय होता, तरी रॅंग्लर र. पु. परांजपे यांच्या शिकवण्याने त्यांना गणिताची आवड लागली होती. ती झाली फार पूर्वीची गोष्ट. सध्या एक-दोन वर्षांपूर्वीच डॉ. मधुमालती आपटे या गणिताच्या प्राध्यापिका स. प. महाविद्यातून फर्ग्युसन कॉलेजमध्ये गेल्या होत्या. या गोष्टीने हुरळून जाऊन मी स. प. महाविद्यालय सोडून फर्ग्युसन कॉलेजमध्ये प्रवेश घेतला, फक्त बी. ए. च्या शेवटच्या वर्षासाठी. तेथे आपटेबाईंनी आम्हाला एकच कोर्स शिकवला. त्यांची शिकवण्याची हातोटी छानच होती. त्यांच्या शिकवण्यात जो एक प्रकारचा ठसका होता, तो मला खूप आवडला. पण एकंदरीत पाहता त्या कॉलेजात असण्याचा पुरेपूर फायदा मला करून घेता आला नाही. आता मागे वळून पाहताना वाटते की मी कॉलेज बदलण्याचा खटाटोप केला नसता तरी चालले असते. पुढे जाऊन पुण्याच्या गणितक्षेत्रात नावारुपाला आलेले स. प. महाविद्यालयामधील प्राध्यापक राईलकर यांची नाराजीही मी ओढवून घेतली नसती.
गणितातील ‘विश्लेषण’ (Analysis) या कोर्ससाठी कुठले तरी पाठ्यपुस्तक नेमले होते, पण मी जी. एच्. हार्डी यांचे ‘A Course in Pure Mathematics’ हे पुस्तक कसोशीने वाचत असे. प्राध्यापक केरकरांनी मला त्याचा परिचय करून दिला होता. गणिताचे पुस्तक वाचताना त्यातील प्रमेये आणि त्यांच्या सिद्धता समजून घेणे हे पहिले आणि मुख्य काम. पण त्यानंतर लेखकाने मानलेली गृहीतके (hypotheses) जास्त व्यापक करता येतील का, किंवा त्याने काढलेले निष्कर्ष अधिक बळकट करता येतील काय असे प्रश्न उभे रहातात. हार्डीने आपले पुस्तक १९०८ साली लिहिले होते आणि प्रस्तावनेत चक्क म्हटले होते की ते पुस्तक विद्यापीठाच्या शिष्यवृत्ती मिळवण्यास पात्र असलेल्या (of scholorship standard) विद्यार्थ्यांसाठीच लिहिले आहे. ते फक्त गणिताच्या अभ्यासकांसाठी होते, इतरांसाठी नव्हे. १९५२ मध्ये त्याची दहावी आवृत्ती केंब्रिज युनिव्हर्सिटी प्रेसने प्रकाशित केली होती. गणिताच्या या भागामधील महत्त्वाच्या सिद्धांतांपैकी एक आहे ‘अव्यक्त फलन सिद्धांत’ (Implicit Function Theorem). हार्डीने आपल्या पुस्तकाच्या दहाव्या आवृत्तीमध्ये हा सिद्धांत अगदी कमी गृहितके मानून सिद्ध केला होता, आणि या कामी प्रा. अब्राहम बेसिकोविच यांची मदत झाल्याचे नमूद केले होते. त्यापेक्षाही कमी गृहितके मानून योग्य ती निष्पत्ति करता येते असे मला दिसून आले. मग मी दोन पानी गणिती मजकूर कुणाकडून तरी टंकलिखित करून घेतला, आणि मनाचा हिय्या करून तो केंब्रिज युनिव्हर्सिटी प्रेसला पाठवला. एक महिना उलटून गेल्यावर मला त्यांचे उत्तर आले. हीच माझ्या दृष्टीने मोठी गोष्ट होती. त्यांनी माझे म्हणणे मान्य केले होते, पण असेही म्हटले होते की मी लिहिलेलीच गोष्ट प्रा. बेसिकोविच् यांनी मांडली असून पुस्तकाच्या १९६३ सालच्या पुनर्मुद्रणात ती समाविष्ट केली आहे. त्यांनी एक ताजी पुनर्मुद्रित प्रत मला पाठवून दिली.
 |
 |
मला फारच आनंद झाला. पण आता लक्षात येते की ही प्रत पाठवून त्यांनी माझी एक प्रकारची बोळवण केली होती, कारण मी दर्शवलेली गोष्ट प्रा. बेसिकोविच यांनी हार्डीला सांगितलेल्या गोष्टीपेक्षा जास्त व्यापक होती. कदाचित मी ओबडधोबड इंग्लिश भाषेत लिहिलेल्या गोष्टी त्यांच्या लक्षात आल्या नसतील. ते कसेही असो, त्यांनी पाठवलेली प्रत मी अजूनही संभाळून ठेवली आहे. फक्त अनेक वर्षे वापरल्यामुळे ती जीर्ण झाली व तिची बांधणी करून घ्यावी लागली.
बी.ए.च्या शेवटच्या वर्षात असताना पुढच्या शिक्षणासाठी अमेरिकेतील काही विद्यापीठांकडे अर्ज करण्याचे मी ठरवले. त्याची दोन कारणे होती. एक म्हणजे आमच्या आधी दोन वर्षे आमच्याच शाळेतून शालांत परीक्षेत पहिला आलेला रवींद्र कुलकर्णी याने गणित विषय घेऊन बी.ए. पदवी मिळवली होती. लगेच अमेरिकेतील हार्वर्ड विद्यापीठात पीएच. डी. करण्यासाठी त्याला शिष्यवृत्ती मिळाली होती. त्याच्या पावलावर पाऊल ठेवून पुढे जायचे ठरवले. त्यानेही मला उत्तेजन दिले. दुसरे असे की माझा मोठा मामेभाऊ मुकुंद जोगळेकर नुकताच पीएच. डी. करण्यासाठी न्यू यॉर्क राज्यातल्या रॉचेस्टर विद्यापीठात गेला होता. तेव्हा आपणही जावे असे वाटले. आता अमेरिकेतील कुठल्या विद्यापीठांत अर्ज करावे? त्याकाळी प्रसिद्ध असलेल्या चार-पाच विद्यापीठांचीच नावे मला माहित होती – हार्वर्ड, प्रिन्सटन, येल, स्टॅनफोर्ड आणि बर्कले (कॅलिफोर्निया). मग या विद्यापीठांत पीएच. डी. करण्यासाठी मी अर्ज केले, आणि शिवाय रॉचेस्टर विद्यापीठाकडे, कारण मुकुंदा तेथे होता. मला सर्वांत आधी रॉचेस्टर विद्यापीठाने शिष्यवृत्ति देऊ केली, इतर विद्यार्थ्यांना द्यायच्या पुष्कळ आधी. त्याचे कारण माझ्या नंतर लक्षात आले. त्या विद्यापीठाच्या अर्जामध्ये एक ऐच्छिक रकाना होता, ज्यात आपण इतरत्र कुठे अर्ज करत आहोत त्याची यादी द्यायची होती. अर्थात् मी त्या जागी पाच सर्वोत्कृष्ट प्रतीच्या विद्यापीठांची नावे लिहिली होती. ती वाचून बहुदा रॉचेस्टरच्या प्रवेशसमितीला असे वाटले असणार की हा विद्यार्थी फारच भन्नाट असला पाहिजे. म्हणून मला चांगली शिष्यवृत्ती देऊन त्यांनी डाव टाकला होता. झाले, मी रॉचेस्टरचा प्रस्ताव स्वीकारूनही टाकला.
काही काळाने मला बर्कले येथील कॅलिफोर्निया विद्यापीठाकडूनही शिष्यवृत्ति मिळाली. त्यावेळी रॉचेस्टरच्या शिष्यवृत्तीऐवजी मी ती स्वीकारू शकलो असतो. पण मी तसे केले नाही, कारण रॉचेस्टरला माझा मामेभाऊ होता ना! प्रथमच इतक्या लांब जायचे तर आपल्यापैकी कोणी तिथे असलेले बरे अशा विचाराने. हा केवढा खुळेपणा होता ते त्यावेळी ध्यानात आले नाही. आज जर कुणा विद्यार्थ्याने बर्कलेला न जाता रॉचेस्टरला जायचे ठरवले तर सगळे मूर्खातच काढतील त्याला.
रॉचेस्टर विद्यापीठात
आई-वडिलांनी विमानाने प्रवास करायची परवानगी न दिल्याने मुंबईहून इटालीमधील जिनोवा नावाच्या बंदरापर्यंत बोटीने, नंतर लंडनपर्यंत मुख्यतः खुष्कीच्या मार्गाने, व परत साऊथहॅम्टनहून न्यूयॉर्कपर्यंत दुस-या बोटीने जावे लागले. शेवटी न्यूयॉर्क ते रॉचेस्टर हा ग्रेहाऊंड बसचा प्रवास. अशी मजल दरमजल करत मी एकदाचा रॉचेस्टरला पोहोचलो, १९६४च्या सप्टेंबर महिन्यात. दुसऱ्याच दिवशी सकाळी माझ्या मामेभावाने मला गणित विभागाच्या इमारतीपाशी नेऊन सोडले. एक तर तीन आठवड्यांच्या प्रवासाने मी अतिशय थकून गेलो होतो, आणि कित्येक नव्या गोष्टी पाहून बावरलोही होतो. बिचकत बिचकत मी गणित विभागाच्या कॉमनरूममध्ये पाऊल टाकले. तिथले दृश्य माझ्या कल्पनेपेक्षा फारच वेगळे होते. सुटाबुटात तर कोणीच नव्हते, उलट टीशर्ट आणि अर्धी चड्डी घालून लोक कॉफी पीत गप्पा मारत होते. माझा नवखा चेहरा पाहून मला कोणीतरी हटकले व आपल्या केबिनमध्ये बोलावले. ते होते माझे शैक्षणिक सल्लागार प्रोफेसर राल्फ रैमी. पहिल्या सेमिस्टरमध्ये मी कोणते कोर्सेस घ्यायचे ते त्यांना ठरवायचे होते. त्यांनी मला मी आत्तापर्यंत काय काय शिकलो असे विचारले. तेव्हा माझी इतकी त त प प झाली की त्यांना मी कोणकोणते कोर्सेस् केले आहेत ते पण धड सांगू शकलो नाही. शेवटी तेच म्हणाले की माझी तयारी अमेरिकन स्नातकपूर्व (undergraduate) विद्यार्थ्याच्या तोडीची दिसत नाही, तेव्हा मी काही बी. ए.च्या स्तरावरील कोर्सेस प्रथम शिकावे. मी अगदी हिरमुसला झालो. पण ते म्हणतील तसे करण्याशिवाय उपायच नव्हता. मला नेमून दिलेल्या चारही विषयांचा मी मन लावून अभ्यास केला आणि चारही विषयांत ‘ए’ ग्रेड मिळवली. दुसऱ्या सेमेस्टरच्या आधी माझे ग्रेड कार्ड प्राध्यापक रैमींनी बघितले आणि म्हटले की माझी कामगिरी चांगली आहे, पण प्रत्येक विषयांत ‘ए’ ग्रेड मिळवलीच पाहिजे असे काही नाही! मग त्यांनी मला एम. एस्सी.च्या स्तरावरील एक कोर्स गाळून एकदम पीएच. डी.च्या स्तरावरील कोर्स करायला सुचवले. असा उंचसखल प्रवास करून चार सेमेस्टरच्या शेवटी मी पीएच्. डी.साठी लागणारे सर्व कोर्सेस पुरे केले.
रॉचेस्टर विद्यापीठातील स्प्रिंग सेमेस्टर जानेवारीत सुरू व्हायचा आणि मे मध्ये संपायचा. मार्चमधील २० तारखेच्या आसपास वसंतऋतु (Spring season) अधिकृतपणे अवतरतो. त्याआधी सगळीकडे बर्फच बर्फ असायचे. रॉचेस्टर गावातून वहाणाऱ्या जेनेसी (Genesee) नदीचे पाणी गोठून जात असे. मी राहत होतो ते अपार्टमेंट नदीच्या एका बाजूला आणि विद्यापीठ पलीकडच्या बाजूला. म्हणून रोज दोनदा नदी ओलांडावी लागे. हिवाळ्यात पुलावरून न जाता गोठलेल्या पाण्यावरून चालत जायला मजा यायची, अंतरही कमी व्हायचे. पण वसंतऋतूची चाहूल लागली की पाणी पुरेसे गोठले आहे की नाही याचा अंदाज घेऊनच पाऊले टाकावी लागत. एकदा नदीचे पाणी खळखळून वहायला लागले की पात्राच्या वरच्या बाजूला एके ठिकाणी वल्ह्याने चालवायची छोटी नाव भाड्याने मिळायची. तिला डोंगी (canoe) असे म्हणत.
1966 साली हे नावेचे दुकान ज्या दिवशी उघडले त्याच दिवशी मी आणि गणित विभागातले माझे दोन मित्र थॉमस गार्नर (Thomas Garner) आणि टॉम लेनर्ड (Tom Lenard) तिथे पोहोचलो. हवेत शिरशिरी होती, पण हिवाळ्याच्या बंधनातून मोकळे व्हायची घाई झाली होती. आम्ही एक डोंगी भाड्याने घेतली आणि नदीत उतरवली. पुढे बसून गार्नर आणि मागे बसून मी वल्हवायला लागलो. लेनर्ड मध्यभागी बसला होता. उंचावरील भागातून नदी सखल भागात येते, आणि मग मी रोज ओलांडून जात असलेल्या पुलाखालून जाते. डावीकडे आमचे अपार्टमेंट, तर उजवीकडे विद्यापीठ. आणखीन पुढे गेले की रॉचेस्टरचे गावठाण (downtown) सुरू व्हायचे. आम्हा तिघांनाही फारच मोकळे, हलके, बंधमुक्त वाटत होते. लवकरच आणखी एक पूल लागला. त्याच्यावर बऱ्यापैकी रहदारी होती. शिवाय सर्वांना दिसेल अशी एक पाटी खांबावर ठोकून लावली होती. तिच्यावर ठळक अक्षरात लिहिले होते ‘नौकानयनाची नाली समाप्त. यापुढे जाऊ नका.’ (End of Navigation Channel. Do not go beyond this point.) आम्ही ती पाटी वाचली. पण पुढून वल्हवणारा गार्नर म्हणाला की अशा पाट्या खूप ठिकाणी असतात, आपल्याला थांबायचे काहीच कारण नाही. उत्साहाच्या भरात मीही त्याला दुजोरा दिला आणि वल्हवणे चालू ठेवले. अशी बंडखोर वृत्ती माझ्यात क्वचितच यायची. मध्ये बसलेल्या लेनर्डने मात्र जास्त सावधगिरी दाखवली. तो म्हणाला तुम्हा दोघांना पुढे जायचे तर खुशाल जा. पण मला मात्र पुलाच्या खांबाजवळ एक चौथरा आहे तिथे उतरू द्या. आम्ही त्याला ‘भागूबाई, भित्रा’ (chicken, chicken) असे चिडवले, पण त्याने मानले नाही. त्याला आम्ही उतरवले, आमच्या खिशातील पैशांची पाकिटे त्याला सुपूर्त केली. पुढे सटकताना त्याला गमतीने असेही म्हटले की आमचे काही बरेवाईट झाले तर ते सगळे पैसे त्याचेच!
आम्ही सावधगिरीने पुढे वल्हवत होतो. जरा लांबवर पाणी एकदम खाली पडताना दिसले. पण आताच परतलो असतो तर आम्हीही भित्रे ठरलो असतो. मग आम्ही ठरवले की जिथून पाणी खाली कोसळत होते त्या कड्याच्या जितक्या जवळ जाता येईल तितके जायचे, नीट धबधबा पाहायचा आणि मगच मागे फिरायचे. हा केवढा चुकीचा विचार होता. मी व गार्नर दोघे गणित विषयात पीएच्. डी. करत असलो तरी आमचे पदार्थविज्ञान (physics) फारच कच्चे होते. जगातील सर्व गतिमान वस्तूंना संवेग (momentum) नावाची चीज असते याचा पार विसर पडला होता. तर काय, जे अटळ होते तेच झाले! तुटलेल्या कड्याच्या पुरेसे जवळ गेल्यावर कितीही प्रयत्न केला तरी मागे येणे अशक्य होते. क्षणार्धात आमची डोंगी धबधब्यावरून खाली
कोसळली. होडी एकीकडे, मी दुसरीकडे आणि गार्नर तिसरीकडे. आमच्या हातातली वल्ही कुठेतरी जाऊन पडली. नदीच्या पात्रांत मोठमोठे खडक होते. त्याच्यावर आपटून किंवा वल्ह्याचा डोक्याला मार लागून आम्ही दोघेही पूर्ण जायबंदी होऊ शकलो असतो. परंतु सुदैवाने असे काही घडले नाही, आम्हा दोघांना फक्त थोडे खरचटले. डोंगी आणि वल्हीही शाबूत राहिली.
पुलाच्या खांबाजवळून लेनर्ड हे सगळे दृश्य बघत होता. त्याला हसू का रडू असे झाले. पण तोच शहाणा निघाला हे नक्की! प्रसंगावधान राखून त्याने अग्निशामक दलाला फोन केला. अर्ध्या तासाच्या आत मोठमोठ्या शिड्या वापरून त्यांनी आम्हाला आणि आमच्या डोंगीला वर काढले, व त्यांच्या नियमाप्रमाणे आम्हाला जवळच्या स्ट्रॉग मेमोरियल हॉस्पिटलमध्ये भरती केले. त्यांनी प्राथमिक उपचार देऊन घरी जाऊ दिले. तेवढ्यात मला एका वर्तमानपत्राचा फोन आला. त्यांना माझी मुलाखत घ्यायची होती. मी सपशेल नकार दिला, ‘काही बोलायचे नाही’ (No comment) एवढेच सांगून. काही जास्त बोललो असतो तर ते माझ्यावरच शेकले असते. ती मोठ्या अक्षरांतील पाटी पुलावर उगाच लावली नव्हती! तरीही दुसऱ्या दिवशी रॉचेस्टरच्या वर्तमानपत्रात आम्हाला वर काढत असतानाचा फोटो आला होता, आणि खाली दिलेल्या बातमीत म्हटले होते ‘रॉचेस्टर विद्यापीठातील दोन विद्यार्थी लाकडी पिंपात (barrel) बसून नायगारा धबधब्यावरून उडी मारण्याचा सराव करत होते!’ गार्नर आणि मी मूग गिळून गप्प बसलो. म्हणतात ना, ‘मौनं सर्वार्थसाधनम्’ म्हणजे गप्प बसले की सगळे साधून जाते! दुसऱ्या दिवशी आम्ही डोंगी आणि वल्ही दुकानदाराला परत नेऊन दिली. त्याने काहीच तक्रार केली नाही, कारण एक तर त्याच्या वस्तूंना काहीच हानी पोहोचली नव्हती, आणि दुसरे म्हणजे वर्तमानपत्रातील बातमीमुळे त्याची गिऱ्हाइके वाढली होती. या प्रसंगाची वाच्यता करायची नाही एवढे मात्र ठरवून टाकले होते. माझ्या आई-वडिलांना हे कधीच कळू दिले नाही. बऱ्याच वर्षांनी काही जुनी कागदपत्रे पहात असताना वर्तमानपत्रातील डोंगीचा आणि माझा फोटो माझ्या पत्नीच्या नजरेस पडला. ती उद्गारली, ‘हे आधी माहीत असते तर अशा अभौतिक माणसाशी मी लग्नच केले नसते.’
दोन वर्षे घरापासून दूर राहिल्यामुळे मला थोडे दिवस भारतात जाऊन यावे असे वाटू लागले. पण तिकडे गेल्यावर कुणी जर दोन वर्षांत काय पदरात पाडून घेतलेस असे विचारले तर त्याला समजेल असे ठोस उत्तर माझ्याकडे नव्हते. मग मी पुन्हा प्राध्यापक रैमींना भेटलो व माझी समस्या सांगितली. ते म्हणाले ‘ओह, तुला एम. ए.ची पदवी पाहिजे आहे का? नो प्रॉब्लेम. एक अर्ज कर आणि दहा डॉलर्स भर की झाले.’ मी एकदम खूष झालो. दहा डॉलरमध्ये एका आठवड्यांत एम. ए.ची पदवी मिळवल्याचे प्रमाणपत्र हातात आले. यामागचे कारण असे होते की एम. ए.साठी जरूर असणारे कोर्सेस मी केव्हाच पार केले होते.

दहा डॉलर्स रॉचेस्टर विद्यापीठाला देऊन पदरात पडलेली एम. ए. पदवी
माझ्या भारतभेटीमध्ये मला माझी एम. ए. पदवी कुणाला दाखवायला लागली नाही हा मुद्दा वेगळा, पण मी ती पदवी घेऊन ठेवली हे चांगलेच केले म्हणायचे. कारण बऱ्याच वर्षांनी एक विचित्र परिस्थिती माझ्या पाहण्यात आली. आर. नरसिंहन नावाच्या विद्यार्थ्याने पर्ड्यू विद्यापीठातील प्राध्यापक श्रीराम अभ्यंकर यांच्या मार्गदर्शनाखाली गणित विषयात पीएच. डी. ही पदवी मिळवली. नंतर 1982 साली भारतात परत येऊन तो मुंबई विद्यापीठात शोधसहयोगी (Research Associate) म्हणून काम करू लागला. त्याच्या कामाचा एक भाग म्हणून तो एम. एस्सी.च्या विद्यार्थ्य़ांना शिकवत पण होता 5 वर्षे. जेव्हा गणित विभागात प्रपाठकाची (Reader) जागा उपलब्ध झाली, तेव्हा नरसीने मुंबई विद्यापीठाकडे अर्ज केला, व बोलावणे आल्यावर मुलाखतीसाठी हजर राहिला. गणितातील विशेषज्ञांनी विचारलेल्या प्रश्नांची नरसीने उत्तम उत्तरे दिली. मुलाखतीच्या शेवटी निवड समितीने त्याने मिळवलेल्या पदव्यांची प्रमाणपत्रे मागितली. पुणे विद्यापीठात बी. ए. केल्यावर तो माझ्यासारखाच तडक पीएच्. डी करायला अमेरिकेला गेला होता. त्यामुळे त्याच्याकडे बी. ए. आणि पीएच. डी. या पदव्यांची प्रमाणपत्रे होते. पण एम. ए. अथवा एम. एस्सी.चे नव्हते. प्रपाठकाच्या जागेसाठी मास्टर्स डिग्री पहिल्या वर्गांत पास होणे ही आवश्यक बाब होती. तेवढ्या कारणाने नरसीची निवड होऊ शकली नाही. केवढे हे नियमांचे अवडंबर! त्या वर्षी नरसी आपण शिकवत असलेल्या विद्यार्थ्यांबरोबर एम. एस्सी. परीक्षेला बसला आणि विशेष प्रावीण्य (distinction) मिळवून पास झाला. परंतु ह्या सर्व घटनांनी त्याला चालू शिक्षणव्यवस्थेचा वीट आला आणि त्याने आपले स्वत:चे ट्युटोरीयल क्लासेस काढले. मी रॉचेस्टर विद्यापीठाला दहा डॉलर्स देऊन एम. ए. पदवी मिळवली असल्याने मला नरसीवर ओढवलेल्या प्रसंगातून जावे लागणार नव्हते.
(पुढील भाग इथे)
---
बालमोहन लिमये
(balmohan.limaye@gmail.com)

लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.
बालमोहन लिमये यांचे इतर लिखाण


प्रतिक्रिया
अतिशय मनोरंजक लेख!
अतिशय मनोरंजक लेख!
> मी म्हटले ‘गणित’. तत्क्षणी त्यांच्या तोंडून ‘अरे बापरे’ असे उद्गार निघाले.
हा अनुभव मलाही आलेला आहे. एक गंमतीदार प्रकार म्हणजे ‘गणितात आपण किती मठ्ठ आहोत’ याबद्दल (काही) लोकांना आपसूकच भरभरून बोलावंसं वाटतं. याउलट समजा एखादी स्त्री भरतनाट्यमचे क्लासेस घेऊन पोट जाळते. तर तिला भेटणारे लोक ‘आता काय बोलायचं मॅडम?! मी कित्ती कित्ती वाईट नाचतो म्हणून सांगू!’ असं म्हणणार नाहीत.
> सरांनी सांगितले की एखादे विधान पहिल्या काही आकड्यांसाठी खरे असले तरी ते प्रत्येक आकड्यासाठी खरे असेलच असे नाही. त्यांनी चटकन उदाहरण दिले. समजा आपले विधान आहे ‘n हा कोणताही आकडा दिला असेल तर 1 ते n पर्यंतच्या सगळ्या आकड्यांचा गुणाकार n या आकड्याच्या घनापेक्षा कमी असतो’, म्हणजे 1 × 2 × ... × (n-1) × n
इथे मजकूर तुटला आहे, पण मुद्दा कळला. उदाहरणार्थ, ५! = १२० ही संख्या ५ च्या घनापेक्षा (म्हणजे १२५ पेक्षा) कमी आहे. पण याउलट १००! ही संख्या १०० च्या घनापेक्षा (म्हणजे दहा लाखांपेक्षा) खूपच जास्त आहे.
> मुंबईहून इटालीमधील जिनोवा नावाच्या बंदरापर्यंत बोटीने, नंतर लंडनपर्यंत खुष्कीच्या मार्गाने
अलिकडे हा शब्द प्रचलित नसल्यामुळे आणि वेगवेगळ्या शब्दकोशांत याचे वेगवेगळे अर्थ देण्याचा रिवाज असल्यामुळे याबद्दल नीट विचार करावा लागला. ‘खुष्कीचा मार्ग’ म्हणजे inland route असा माझा समज आहे. पण अर्थात फ्रान्सच्या पश्चिम किनाऱ्यापर्यंत आल्यानंतर इंग्लंडला जाण्यासाठी पाण्यात शिरावं लागणार. (अलिकडे रेल्वे असते, पण तेव्हा नव्हती.)
> कारण बऱ्याच वर्षांनी एक विचित्र परिस्थिती माझ्या पाहण्यात आली. आर. नरसिंहन नावाच्या … त्याच्याकडे बी. ए. आणि पीएच. डी. या पदव्यांची प्रमाणपत्रे होते. पण एम्. ए. अथवा एम्. एस्सी.चे नव्हते. प्रपाठकाच्या जागेसाठी मास्टर्स डिग्री पहिल्या वर्गांत पास होणे ही आवश्यक बाब होती. तेवढ्या कारणाने नरसीची निवड होऊ शकली नाही.
हा नियम प्राचीन काळी कुठल्यातरी खाकी डोक्याच्या नोकरशहाने आणला असणार. अजूनही तो लागू होतो का ते ठाऊक नाही. पण मीही अमेरिकेत पीएचडी करत असताना तो उडत उडत ऐकला होता, आणि इन्शुरन्स पॉलिसी म्हणून मीही तुमच्याचप्रमाणे एक फॉर्म भरून, त्यावर मी केलेल्या कोर्सेसची यादी लिहून मास्टर्स डिग्री घेऊन ठेवली होती. (पण त्याला पैसे वगैरे द्यावे लागले नाहीत.) उत्तर अमेरिकेत मात्र एकदा पीएचडी मिळाली की मास्टर्सबद्दल कुणी विचारत नाही.
- जयदीप चिपलकट्टी
(होमपेज)
दुरुस्ती
आभार! आता दुरुस्ती केली आहे.
.
>>> गंमतीदार प्रकार म्हणजे ‘गणितात आपण किती मठ्ठ आहोत’ याबद्दल (काही) लोकांना आपसूकच भरभरून बोलावंसं वाटतं.
मी कालच हा लेख वाचला. आणि इथे येऊन मी गणितात किती मठ्ठ आहे हे भरभरून बोलणार होते. पण आता नाही बोलणार.
मला वाटतं की परीक्षेसाठी म्हणून अभ्यास करावा लागतो तेव्हा गणितासारख्या विषयांबद्दल जास्त भीती वाटते. पण गणित जेव्हा इतर विषयांसाठी म्हणून शिकावं लागतं तेव्हा तसं होत नाही.
गणित विरुद्ध भरतनाट्यम्
तुलना विनोद ह्मणून ठीक, पण भरतनाट्यम (किंवा तत्सम इतर काही) प्रत्येक व्यक्तीस शाळेत दहावीपर्यंत सक्तीचे नसते, त्याच्या सतत परीक्षा होऊन नापास होण्याची किंवा कमी मार्क मिळण्याची सार्वत्रिक भीती नसते. आणि मुख्य ह्मणजे भरतनाट्यम मधे ‘ढ’ असल्याने दैनंदिन जीवनात कसलीच अडचण येत नाही. त्यामुळ “आपल्याला भरतनाट्यम येत नाही किंवा समजतही नाही” याची खंत वाटण्याची सुतराम शक्यता नसते. गणिताच्या बाबतीत हे सगळेच होते. त्यामुळे गणितज्ज्ञांबद्दल भीतीयुक्त आदर जनसामान्यांत असणे समजण्यासारखे आहे असे मला वाटते.
….शेवटी मदांध तख्त फोडते मराठी!
गणित विषय इतर शास्त्र
गणित विषय इतर शास्त्र विषयांच्या (आणि इतरही अनेक व्यासंगाच्या) मानाने बराच वेगळा आहे याची जाणीव मला एका हैदराबाद सीसीएमबी मध्ये काम करणाऱ्या एका बऱ्याच श्रेष्ठ सायंटिस्टने बऱ्याच वर्षे पूर्वी करून दिली होती. पुष्कळ लोकांना गणित म्हणजे पटपट बेरीज-वजाबाकी-गुणाकार-भागाकार करणे असेच वाटते. माझा एक मित्र एके काळी 'तुम्ही लोक' जास्त कोनांची ट्रिगॉनॉमेट्रिक टेबले काढता का किंवा आणखी क्लिष्ट (?) लॉगटेबले तयार करता का असे विचारत असे. यामुळेच पुष्कळ कॉमर्स आणि अकाउंटिंग वाले लोक 'मी गणितात कसा चांगला होतो' असे सांगतात. मला वाटते लिमयेसर याबद्दल जास्त विस्ताराने लिहू शकतील.
अर्थात भरतनाट्यम हे गणितापेक्षा बरेच अवघड आहे असे मला वाटते!
शरद साने
असू शकते!
कॅामर्स आणि अकौंटन्सी मधील काही लोकांचे गणित “चांगले” असू शकते. त्यात ‘quantitative feel’ चांगला असणे, संख्यांबद्दलची intuition असणे, आणि क्लिष्ट (त्यांच्या क्षेत्राच्या संदर्भात) आकडेमोड अचूक आणि जलद करता येणे, ह्या क्षमता गणितीच नव्हेत काय? Financial markets चे अर्थशास्त्र आजकाल बरेच गणित वापरते, आणि ती prowess काही गुंतवणूकदारांच्या यशापयशात महत्त्वाची ठरू शकते. Forensic accounting मध्येही आजकाल बरेच प्रगत गणित वापरतात.
अर्थात प्रगत गणित आणि गणिती कुशलता यांच्या व्याख्या तुम्ही काय करता यावर तुमची judgements अवलंबून असणारच.
असो.
….शेवटी मदांध तख्त फोडते मराठी!
बुद्धी आणि कौशल्य
आता लोकांच्या हातात, खिशात, पर्शीत उत्तम कॅमेरे असतात. मग हुबेहूब दिसतं तसं चित्र काढणं ही कला म्हणायची का कौशल्य? सतरा किंवा सत्तावीसचा पाढा येत नसला तरी आपल्या हातातल्या कॅमेऱ्यातून काय चित्रं टिपली जात आहेत याकडे किंचित दुर्लक्ष करून १७ * २७ हे उत्तर सहज काढता येतं, मग ते पाढे म्हणणं ही बुद्धी का कौशल्य?
माझे मित्र, नातेवाईक मला धडाधड कोव्हिडसंबंधित आकडे वाचून दाखवतात, आणि मी त्यावर मान हलवून 'मला हे काही समजत नाही' म्हणते. मला ते आकडे समजतात. पण त्यांचा अर्थ काय लावायचा हे समजत नाही. हॉस्पिटलं किती भरली आहेत, किती लोकांनी लशी घेतल्या आहेत, वगैरे वगैरे बरेच प्रश्न मला पडतात आणि त्या आकड्यांचा अर्थ मला लावता येत नाही. "आज आमच्या शहरात ३१४ रुग्ण सापडले" याचा मला काहीही अर्थ लागत नाही.
आकडेमोड निराळी आणि गणित निराळं; आकड्यांचा अर्थ लावता येणं आणखी निराळं. आकडेमोड मीसुद्धा करते, पण त्यासाठी मी कोड लिहिते. पण त्यातून जे आकडे बाहेर येतात, त्याचा अर्थ, भौतिक जगातला संदर्भ मला समजला तर मला आकडे समजले असं मी म्हणते. नाही तर कॅलक्युलेटर आणि माझ्यात काय फरक राहिला?
---
सांगोवांगीच्या गोष्टी म्हणजे विदा नव्हे.
आकडेमोड हा गणिताच्या मुख्य
आकडेमोड हा गणिताच्या मुख्य गाभ्यामधील एक घटक झाला. तो त्याचे सर्वस्व नाही. याच कारणाने शकुंतला देवी या थोर गणितज्ञ वगैरे नाहीत.
शरद साने
शकुंतला देवी या थोर गणितज्ञ असं कोण म्हणतं?
६७-६८ मध्ये यांचा उदय झाला आणि आमच्या शाळेत त्यांना बोलावलं होतं. मोठमोठ्या बारा आकडी संख्याचे गुणाकार भागाकार हाताने करून आमच्या गणिताच्या मास्तरांनी उत्तरं तयार ठेवलेली. ती गणितं विचारल्यावर शकुंतला बाईंनी धडाधड उत्तरं सांगितली होती. अर्थात गणिती म्हणून नव्हे तर एक सिद्धी प्राप्त असेच पाहिले होते.
मास्टर्सबद्दल...
आमच्या ऑफिसात उन्हाळ्यात इंटर्न लोक कामाला आले होते. त्यांनाही शंका असतात म्हणून पचडी केलेल्या लोकांशी गप्पांचा एक कार्यक्रम ठेवला होता. त्यात या मुलांना सगळ्यांनी हाच सल्ला दिला. हौस असेल तर पीएचडीला प्रवेश घ्या, कंटाळा आला तर किमान मास्टर्स पदवी पदरात पाडून घ्या!
लेख आवडलाच.
---
सांगोवांगीच्या गोष्टी म्हणजे विदा नव्हे.
पुन:प्रत्ययाचा आनंद
मलाहि हा लेख आवडला, अशामुळे की त्यातून मला पुन:प्रत्ययाचा आनंद मिळाला.
बालमोहन लिमये ह्यांनी एसपी आणि फर्ग्युसनचा जो काळ वर्णिला आहे त्याच सुमारास मीहि फर्ग्युसनमध्ये गणिताचा अभ्यास करीत होतो आणि संस्कृत हा माझाहि आवडता विषय होता. मी लिमयेंच्या दोन किंवा तीन वर्षे पुढे होतो.
विद्यार्थी साहाय्यक समितीच्या मदतीसाठी त्यांच्या बोलावण्यावरून मी प्रा. केरकरांच्या बंगल्यावर गेलो होतो तेव्हा सुमित्राबाई आणि अच्युतराव आपटे ह्यांनी माझा इंटरव्हयू घेतला होता. माझ्या शिक्षणासाठी मला समितीचा खूप लाभ झाला. तदनंतर थोड्याच दिवसात प्रा. मधुमालती आपटे एसपी मधून आमच्या कॉलेजात आल्या आणि आम्हास Projective Geometry शिकवू लागल्या. तदनंतर मी विद्यापीठात जाऊ लागलो तेथेहि त्या आम्हास Algebraic Projectve Geometry शिकवत असत असे अंधुक स्मरते. प्रा.अ.भि.शहा आणि मधुमालती आपटे ह्यांचे Coordinate Geometry वरचे पुस्तक त्या काळात बरेच विद्यार्थिप्रिय होते. (प्रा.अ.भि.शहा समाजवादी कार्यकर्ते होते आणि ते अल्पवयातच वारले.) सध्याची प्रख्यात अभिनेत्री राधिका आपटे ही मधुमालती आणि अच्युतराव आपटे ह्यांची नात आणि तिच्या चेहऱ्यात मला तिच्या आजीचा भास होतो. आपटेबाईंची एक सवय मला अजून आठवते. फळ्यावर त्यांनी काही लिहिले आणि त्यावर विचार करू लागल्या म्हणजे त्या स्वत:शीच काहीतरी गाणे गुणगुणत असत.
रीसर्च पेपर्स
‘Mathematical Reviews’ ह्या डेटाबेसवर मला अच्युत आणि मधुमालती आपटे ह्या दोघांचे रीसर्च पेपर्स पाहता आले. १९५१ ते १९५७ ह्या काळात अच्युतरावांनी मॅथमॅटिकल फिजिक्स ह्या विषयावर चार पेपर्स लिहिले आहेत. १९५४ ते १९५६ या काळात मधुमालतीबाईंनी डिफरन्शिअल जॉमेट्रीवर चार पेपर्स लिहिले आहेत. दोघांनी एकत्र काम केलेलं मात्र दिसत नाही. एक वैशिष्ट्यपूर्ण बाब म्हणजे हे सगळे पेपर्स फ्रेंचमध्ये आहेत. फ्रान्समध्ये कुठेतरी ते एकत्र शिकायला असावेत अशी एक शक्यता वाटते.
- जयदीप चिपलकट्टी
(होमपेज)
गणिताच्या निमित्ताने - भाग १
गणिताची अशी सुरेख ओळख
आमच्या लहानपणी जर कोणी करून दिली असती तर …
दीपक फाटक
अच्युतराव आणि मधुमालती आपटे
@जयदीप चिपलकट्टी - "फ्रान्समध्ये कुठेतरी ते एकत्र शिकायला असावेत अशी एक शक्यता वाटते."
ते दोघेहि फ्रान्समध्ये एकत्र शिकायला होते - Université de Paris. विद्यार्थी साहाय्यक समितीची कल्पना अच्युतरावांना तेथेच सुचली. आर्थिक कुवत कमी असलेले विद्यार्थी तेथे 'कमवा आणि शिका' ह्या पद्धतीने शिक्षण घेत असत. तीच पद्धत वापरून त्यांनी पुण्यात समितीची स्थापना केली.
मधुमालतींच्यावर स्त्री मासिकात आलेला एक लेख मी शाळेत असतांना वाचलेला होता. त्यंचे तेव्हाचे आडनाव 'धोपेश्वरकर' होते असे वाचल्याचे स्मरते.
बोटीचा प्रवास
जुन्या पिढीतल्या मंडळींना एक विनंती: भारतातून विलायतेला बोटीने जाण्यासंबंधीचे सविस्तर अनुभव नक्कीच वाचायला आवडतील. म्हणजे बोटीवर वातावरण कसं असत असे, जेवणाची (आणि वाईनची वगैरे) सोय काय असायची, प्रवासखर्च किती होता, गौरवर्णीय-गौरेतर मंडळी एकमेकांत कितपत मिसळत असत, बोटीवर वेगवेगळ्या सामाजिक स्तरांमधला फरक कितपत जाणवत असे, असं सगळंच. ‘ऐसी’वर अर्थात परदेशात जाऊन आलेले किंवा परदेशात राहणारे लोक खूपच आहेत, पण बोटीने तिकडे गेलेले अतिशय कमी संख्येने असणार.
- जयदीप चिपलकट्टी
(होमपेज)
विलायतेचा बोटप्रवास.
<भारतातून विलायतेला बोटीने जाण्यासंबंधीचे सविस्तर अनुभव नक्कीच वाचायला आवडतील.>
अशा प्रकारचे एक वर्णन डॉ.पां.दा.गुणे लिखित ’माझा युरोपातील प्रवास’ ह्या पुस्तकामध्ये वाचता येईल. पुस्तक येथे उपलब्ध आहे.
डॉ.पां.दा.गुणे (१८८२-१९२२) हे ब्रिटिश सरकारची शिष्यवृत्ति घेऊन जर्मनी येथे लाइप्झिग विद्यापीठात भाषाशास्त्र (Philology) ह्या विषयाच्या अभ्यासासाठी गेले होते. ते तिकडे युरोपामध्ये १९१०-१३ ह्या काळात होते. त्यांनी आपल्या स्नेह्यांना लिहिलेल्या प्रवासवर्णनपर पत्रांवरून हे पुस्तक तयार केले गेले आहे.. त्या तीन वर्षांमध्ये त्यांनी युरोपातील अनेक देशांचा प्रवास केला. पहिल्या महायुद्धापूर्वीचा युरोप कसा होता ह्याचे दर्शन ह्या पुस्तकावरून आपल्याला होते.
डॉ.पां.दा.गुणे हे पुण्यामधील प्रख्यात भांडारकर प्राच्यविद्या संशोधन संस्थेच्या संस्थापकांपैकी एक होते आणि संस्थेचे पहिले चिटणीस होते..
मनोरंजक होणार ही लेखमाला.
मनोरंजक होणार ही लेखमाला.
गणित आणि इतर गमतीजमती वाचायला आवडतात.
आर्टसकडून गणित विषय घेतल्याने सायन्सच्या दीर्घ अभ्यासक्रमातून मुक्तता होते.
माझा युरोपातील प्रवास’ पुस्तकही उतरवले. चांगले सवाचारशे पानांचे आहे.
इन्डक्शन पद्धत फार
इन्डक्शन पद्धत फार व्हर्सेटाइल आहे. अतिशय आवडती पद्धत होती.
लेख फार आवडला.
बदल
आकडे लिहिण्याच्या पद्धतीत बदल केला आहे
https://www.loksatta.com
https://www.loksatta.com/sampadkiya/visheshlekh/iit-reformer-youth-revol...
वरील लेखात श्री. बालमोहन लिमयेंचा उल्लेख आढळला.
"ऑल रोड्स लीड टु रोम!" हा लेख कुठे वाचायला मिळेल?
DROUGHT RELIEF-A First-Hand
DROUGHT RELIEF-A First-Hand Account हा तो मूळ इंग्रजी लेख असावा.
Deleted
Deleted
संदर्भ
Draught Relief: A First-Hand Account, Economic and Political Weekly, Vol 6, Issue 41, dated 9 October 1971
https://www.epw.in/journal/1971/41/our-correspondent-columns/drought-rel...
प्राध्यापक मनोहर राइलकर यांनी
प्रा. राईलकरांचे काल (३१.८.२०२२) रोजी राहत्या घरी वृद्धापकाळाने ( वय९२) निधन झाले. ते शेवटपर्यंत कार्यरत होते- गतवर्षी शालेय मुलांसाठी त्यांनी लिहिलेल्या पुस्तकांचे प्रकाशनही झाले होते.
The Journey Is the Reward...