गणित म्हणजे काय?

बालमोहन लिमये

शाळेत आपण शिकतो त्या विषयांपैकी गणित हा एक विलक्षण विषय आहे. विद्यार्थ्याची हुशारी बऱ्याच वेळा त्याला गणितात किती गुण मिळतात यावर ठरवली जाते, इतर विषयांनी काही फरक पडत नाही. “आमचा आनंदा हुशार आहे हो, त्याला नेहमी गणितात पैकीच्या पैकी गुण मिळतात”, असे उद्गार आपल्याला खूप वेळा ऐकू येतात. त्यामुळे गणितात प्रावीण्य असणे हा मानाचा भाग बनून जातो. पण अशा प्रवीण मुलांपैकीही फारच थोड्यांना गणितात गोडी असते, बाकी सगळे गणिताकडे उत्तम गुण मिळवून देणारा विषय, म्हणजे एक दुभती गाय, याच दृष्टीने बघत असतात. वर्गातील बहुसंख्य मुलांना तर गणिताची भीतीच वाटत असते. मी शाळेतून बाहेर पडायला आता साठ-पासष्ट वर्षे झाली तरी तेव्हाची आणि सध्याची परिस्थती सारखीच आहे. पुढील आयुष्यात देखील, प्रत्यक्ष गणित शिकवणारे किंवा त्यात संशोधन करणारे असे अगदी थोडे लोक सोडून, इतर सगळे जण गणिताला वचकूनच असतात. विशेषतः कला-वाङ्मयीन वा वैद्यकीय व्यवसाय करणारे तर गणिताचा वासही आला तर तोंडच फिरवतात; अभियांत्रिकी कामे करणाऱ्यांतसुद्धा गणिती माणसाचा एक प्रकारचा दबदबा असतो. अशा गणित या अनोख्या विषयाच्या काही मूलभूत पैलूंसंबंधी चर्चा करायची आहे. गणिताची व्याख्या करू पाहणे दुरापास्त आहे. कितीही प्रयत्न केला तरी अशक्य कोटीतले होऊन जाते. शेवटी गणितज्ञ जे करतात ते गणित असे म्हणण्याची पाळी येते. पण मग गणितज्ञ कुणाला म्हणायचे, तर जे गणित या विषयात काम करतात ते! मात्र असा वर्तुलीय विचार (circular reasoning) करून काहीच फायदा नाही; त्यापेक्षा गप्प बसलेले बरे!

गणित आले कुठून?

गणित शब्दाचा अर्थ गणना केलेले किंवा मोजलेले, आकडेमोड केलेले असा आहे. मोजमापासंबंधी ज्या शास्त्रात चर्चा होत असे, त्या अंकशास्त्राला सुरुवातीच्या काळात गणित म्हणत. आता शालेय चौकटीमध्ये a, b अशा अव्यक्त राशींची चिह्नमोड करणारे बीजगणित आणि त्रिकोण, वर्तुळ अशा आकृतींना अभ्यासणारे रेखागणित म्हणजेच भूमिती यांचाही समावेश गणितात होतो. पण गणित या विषयाचा आवाका याहून फार मोठा आहे. त्याच्या उपभागांची जंत्री येथे न देता आपण त्याची सुरुवात कशी होते ते पाहू या. अगदी लहान असल्यापासून ‘किती?’ या प्रश्नाचे उत्तर देता देता आपल्यात संख्यांची जाणीव (numerosity) निर्माण होत असते. तिच्यामुळेच आपण कुठल्याही गोष्टी 1, 2, 3, 4 अशा सहजपणे मोजू लागतो. म्हणून या संख्यांना ‘नैसर्गिक संख्या’ (natural numbers) असे म्हणतात. त्यांच्या बेरीज, वजाबाकी, गुणाकार, भागाकार, वर्गमूळ, घनमूळ इत्यादी क्रियांतून अंकगणिताचा पसारा निर्माण होतो. येथे एक महत्त्वाची गोष्ट नमूद करणे गरजेचे आहे. लहान मुलाला बेरीज शिकवताना आपण 10 + 5 = 15 असे सांगतो कारण आपल्याकडे आधी 10 आंबे असले, नंतर आणखी 5 आंबे आणले व ते सगळे एकापुढे एक मांडून मोजले तर ती गणना 15 पर्यंत येऊन थांबते. या प्रकारे बेरीज करायची हे आपण सगळ्यांनी म्हणजे अख्ख्या मानवसमाजाने ठरवले आहे, म्हणून आपण आपल्या मुलामुलींना तसे बेधडक शिकवतो, व तेही चुपचाप ऐकतात. पण खरा मुद्दा असा आहे की, ही बेरजेची व्याख्या आपणच निर्माण केली आहे, ती देवदत्त (God given) किंवा निसर्गदत्त नाही. आपण कुठल्याही दोन नैसर्गिक संख्यांची ही नेहमीची बेरीज करू शकतो कारण आपल्याकडे नैसर्गिक संख्यांचा अमाप पुरवठा आहे, त्या कधी संपत नाहीत म्हणून.

पण समजा, आपल्याकडे थोड्याच नैसर्गिक संख्या असल्या तर कशी बेरीज करायची? उदाहरणार्थ, घड्याळाच्या तबकडीवर बाराच आकडे असतात, म्हणून 12 वाजून 1 तास झाला की 13 नाही वाजत, तर 1 वाजतो. याचा अर्थ, 12 वाजणे आणि 0 वाजणे दोन्ही समान समजले जाते. तेव्हा घड्याळाच्या संदर्भात 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 असे बाराच आकडे आहेत, आणि यांपैकी कुठल्याही दोन अंकांची बेरीज केली तर या बारा आकड्यांपैकीच एक अंक मिळतो. मग या नव्या बेरजेची व्याख्या कशी करता येईल? एक सोपा मार्ग असा आहे. घड्याळावर हे बारा आकडे गोलाकार क्रमाने काढायचे, म्हणजे नेहमीच्या 12च्या जागी 0 हा आकडा काढायचा इतकेच. 10 आणि 5 यांची नवी बेरीज करायची म्हणजे 10 वाजल्यानंतर 5 तास गेले की जितके वाजतील ते उत्तर, म्हणजे 3 हे उत्तर मिळते. वस्तुतः ही नवी बेरीज आपण सदानकदा करत आलेलो आहोत, जसे शाळेला 10 वाजता जायचे आणि 5 तासांची शाळा संपली की 3 वाजता घरी यायचे असे आपण म्हणतो. अशीच इतर कुठल्याही दोन आकड्यांची नवी बेरीज करता येते, 12 आणि 0 यांना समान राखून. तिला ‘घड्याळावरची बेरीज’ असे नाव देता येईल.

आता वरील क्रिया 12ऐवजी आणखी कुठल्याही नैसर्गिक संख्येला आणि 0 या संख्येला समान राखून करता येईल. खरोखर, आपण व्यवहारात अशा प्रक्रिया करत आलेलो आहोत : विमान कंपन्यांच्या वेळापत्रकांत 24 तासांचे घड्याळ वापरतात तेव्हा 24 आणि 0 यांना समान राखले असते; तसेच गुरुवारनंतर 5 दिवसांनी मंगळवार येतो असे जेव्हा आपण म्हणतो तेव्हा सातवा वार रविवार हा शून्यवा वार आहे असे आपण धरतो, म्हणजे 7 या संख्येला आणि 0 या संख्येला समान राखतो, किंवा ऑक्टोबर महिन्यानंतर 4 महिन्यांनी मार्च महिना येतो असे म्हणताना आपण बारावा महिना डिसेंबर हा शून्यवा महिना आहे असे धरतो, म्हणजे 12 या संख्येला आणि 0 या संख्येला समान राखतो. आपल्याला माहीतच आहे की घरातील विजेचे जाळे, मिश्रणयंत्र (mixer), संगणक (computer) अशा कुठल्याही विजेच्या कळीने (electric switch) चालणाऱ्या उपकरणाला फक्त दोनच आकडे कळतात, बंद म्हणजे 0 आणि चालू म्हणजे 1. बंद असलेले बटन दाबले की ती कळ चालू होते, व ते पुन्हा दाबले की बंद पडते; म्हणजे 1 अधिक 1 बरोबर 0. याचा अर्थ, ती कळ वापरताना आपण 2 आणि 0 या संख्यांना समान राखतो. तेव्हा 1 अधिक 1 बरोबर 2 अशी काही काळ्या दगडावरची रेघ नाही, 1 अधिक 1 बरोबर 0 देखील होऊ शकते. आहे की नाही गंमत?

बेरजेप्रमाणेच वजाबाकी, गुणाकार, भागाकार या क्रियाही अशा वेगळ्या प्रकारांनी करता येतात. या चक्रीय धाटणीच्या (cyclic pattern) अंकगणिताला भाजक अंकगणित (modular arithmetic) असे नाव आहे. त्याचा मोठा उपयोग संकेतन (coding) करण्यासाठी आणि क्रमसंख्येचा अवेक्षणांक (check digit of a serial number) ठरवण्यासाठी होतो. या सगळ्या चर्चेतील पायाभूत गोष्ट म्हणजे बेरजेसारख्या बैजिक क्रिया आणि सामान्यतः गणितातील सर्वच प्रक्रिया कशा करायच्या ते माणूस ठरवत असतो, त्या काही आभाळातून पडलेल्या नसतात.

मूळ संख्या

पाचवीच्या गणितात आपल्याला मूळ संख्यांचा परिचय होतो. नैसर्गिक संख्यांपैकी या काही खास संख्या आहेत. जी नैसर्गिक संख्या 1पेक्षा मोठी आहे आणि जिला इतर कुठल्याही संख्येने भाग जात नाही (फक्त 1 आणि ती संख्या सोडून) तिला ‘मूळ संख्या’ (prime number) असे म्हणतात; म्हणजे 2, 3, 5, 7, 11, 13 इत्यादी. सातवीत आपण शिकतो की कुठलीही नैसर्गिक संख्या एक तर मूळ संख्या असते किंवा काही मूळ संख्यांचा गुणाकार करून मिळवता येते; या मूळ संख्यांना दिलेल्या संख्येचे मूळ अवयव (prime factors) म्हणतात, जसे 12 = 2 × 2 × 3 किंवा 35 = 5 × 7, आणि म्हणून 12 या संख्येचे 2, 2 व 3 हे मूळ अवयव आहेत, तर 35 या संख्येचे 5 व 7 हे मूळ अवयव आहेत. इसवी सनापूर्वी 300 वर्षे आधी युक्लिड या ग्रीक गणितज्ञाने म्हटले की, आपल्याला जास्त जास्त मोठ्या मूळ संख्या नेहमीच मिळत राहतील. हे विधान त्याने एका फार सोप्या व सुटसुटीत रितीने दाखवून दिले. जागतिक गणितातील हा एक अतिशय सुंदर युक्तिवाद मानला जातो. तो इथे सांगितल्याविना मला राहवत नाही. कुठलीही n ही नैसर्गिक संख्या घ्या. आपण दाखवणार आहोत की n पेक्षा मोठी एखादी तरी मूळ संख्या असलीच पाहिजे. आता n पर्यंतच्या सगळ्या मूळ संख्यांचा गुणाकार करा व त्यात 1 मिळवा. या भल्या मोठ्या संख्येला एक तरी मूळ अवयव असला पाहिजे. शिवाय हा मूळ अवयव n पेक्षा कमी किंवा n एवढा असू शकत नाही, कारण n पर्यंतच्या सगळ्या मूळ संख्यांच्या गुणाकारात आपण 1 मिळवला आहे ना! म्हणून तो मूळ अवयव ही n पेक्षा मोठी मूळ संख्या झाली. खेळ खलास! याचा अर्थ मूळ संख्या कधीच संपत नाहीत; त्या अनंत आहेत.

दोनचा फरक असलेल्या मूळ संख्यांच्या किती तरी जोड्या आपल्याला आढळून येतात, जसे 3 व 5, 5 व 7, 11 व 13, 17 व 19, वगैरे. अशा जोड्यांना जुळ्या मूळ संख्या (twin primes) म्हणतात. जशा मूळ संख्या कधीच संपत नाहीत, तशा जुळ्या मूळ संख्या नेहमीच मिळत राहतील की त्या संपून जातील? हा सवाल प्रथम 1850 सालाच्या सुमारास म्हणजे जवळजवळ 175 वर्षांपूर्वी एका फ्रेंच गणित्याने केला होता. पण उत्तमोत्तम गणितज्ञांना याचे उत्तर अजून मिळालेले नाही. युक्लिडने जसे मूळ संख्या अनंत आहेत हे दाखवले तसे कोणी दाखवू शकले नाही की जुळ्या मूळ संख्या अनंत आहेत, व कोणी असेही दाखवू शकले नाही की जुळ्या मूळ संख्या एका मर्यादेनंतर मिळणार नाहीत. हा प्रश्न गणितातील अगदी सोपेपणे विचारता येणाऱ्या पण त्याचे उत्तर माहीत नसलेल्या प्रश्नांपैकी एक आहे. खरोखर, गणित हा विषय जिवंत आहे, त्यात असे संशोधन करायला खूप वाव आहे.

कित्येकांना वाटेल की मूळ संख्यांचा अभ्यास कशासाठी करायचा, त्यातून काय फायदा होतो? प्रामाणिकपणे सांगायचे झाले तर, अशा कुठल्या नफ्यासाठी गणितज्ञ आपले पुरे जीवन या प्रश्नांवर वाहून टाकत नाहीत. ते त्यांची नैसर्गिक उत्सुकता शमवण्याचा प्रयत्न करत असतात, त्यातून त्यांना निर्भेळ आनंद मिळत असतो. मात्र, आतापर्यंतच्या इतिहासावरून असे दिसते की, अशा निरिच्छ प्रयासांतून अनपेक्षितपणे काही तरी निघते व त्याचा फार मोठा उपयोग होऊ लागतो. मूळ संख्यांबाबत असेच झाले आहे. गूढलेखनात (cryptography) आपण पाठवलेला संदेश ज्याच्यासाठी आहे त्यालाच समजावा, इतर कुणाला समजू नये याची काळजी घ्यावी लागते. आर-एस-ए गूढपद्धतीत (RSA cryptosystem) ही खबरदारी अशी घेतात : दोन मोठ्या मूळ संख्या मनाशी बाळगायच्या आणि ज्याला संदेश पाठवायचा आहे त्याला त्या सांगून ठेवायच्या. या मूळ संख्यांचा गुणाकार करून जी अवाढव्य संख्या मिळेल, ती वापरून सांकेतिक (coded) संदेश पाठवायचा. ही अवाढव्य संख्या इतरांना कळली तरी हरकत नाही, कारण संदेशातील संकेत समजण्याची गुरुकिल्ली (decoding key) आपण मनात बाळगलेल्या दोन मूळ संख्या हीच असते, व इतर कुणाला ती मिळवणे अशक्य कोटीतले होते. म्हणून आपला संदेश केवळ इच्छित माणसालाच समजू शकतो. उदाहरणार्थ, 193,707,721 आणि 761,838,257,287 या मूळ संख्यांचा गुणाकार करणे तसे सोपे आहे, निदान संगणकाला तरी; तो गुणाकार आहे 147,573,952,589,676,412,927. आता या 21 आकड्यांच्या भल्या मोठ्या संख्येला फक्त दोनच मूळ अवयव आहेत, व तेही खूप मोठे आहेत, म्हणून ते शोधून काढणे प्रगत संगणकालाही जमत नाही. त्यामुळे आपला संदेश आपण ज्याला ते मूळ अवयव आधीच सांगून ठेवले असतील त्यालाच समजू शकतो.

भारतीय गणितज्ञांमध्ये श्रीनिवासन रामानुजन अग्रस्थानी आहेत. त्यांचे अभिजात बुद्धिवैभव प्रकट करायला प्राध्यापक जी. एच. हार्डी या केंब्रिज विद्यापीठात (University of Cambridge) काम करणाऱ्या इंग्लिश गणितज्ञाने मोठा हातभार लावला. ते विख्यात अंकशास्त्रज्ञ होते. त्यांचा दावा होता की त्यांनी केलेल्या कुठल्याच कामाचा काहीही उपयोग होणे अशक्य आहे. पण त्यांच्याच उत्तरायुष्यात मूळ संख्यांचे गूढलेखनात उपयोजन होऊ लागले. ते पाहून त्यांना चक्क वाईट वाटत असे. ते म्हणायचे, “अरेरे, निव्वळ कुतूहल शमवण्यासाठी आपण केलेले प्रयास अशा गौण गोष्टी साध्य करण्यास वापरले जावेत, यापरते दुःख नाही!” आता काय म्हणाल?

गणित व संगणकशास्त्र

खूप वर्षांपूर्वी, संगणकांचा वापर सुरू होत होता तेव्हा मला कुणी म्हटले की आता संगणकांकडून इतकी पटापट व बिनचूक उत्तरे मिळू लागतील की गणित शिकायची गरजच भासणार नाही. संगणकांमुळे रोजच्या व्यवहारांमध्ये क्रांती झाली आहे, हे मान्य. पण संगणक कितीही स्मृतिवान व गतिमान असला तरी त्याला माणूस करू शकतो तसा युक्तिवाद करता येत नाही. एखादी खूप मोठी संख्या ही मूळ संख्या आहे की नाही असे संगणकाला विचारले आणि त्याला पुरेशी स्मृती आणि वेळ या गोष्टी दिल्या, तर तो निश्चित उत्तर देईल; पण एकूण मूळ संख्या अनंत आहेत का नाहीत हा प्रश्न संगणकाला सोडवता येणे शक्य नाही. याचे कारण असे की उत्तर हो किंवा नाही कसेही असले तरी ते देण्यासाठी अनंत शक्यता लक्षात घ्याव्या लागतात, व हे काम संगणकाच्या मर्यादेबाहेरचे आहे. त्यासाठी गणिती विचारसरणीच आवश्यक आहे. अगदी अलीकडच्या काळात कृत्रिम बुद्धी (Artificial Intelligence) ह्या संगणकशास्त्रातल्या अभ्यासक्षेत्राचा बोलबाला होत आहे, चॅटजीपीटी (ChatGPT) नावाची मानवी संवादाचे हुबेहूब अनुकरण करणारी मृदुसामग्री (software) पुढे येत आहे. ती मानवानेच अगोदर निर्माण केलेल्या भाषेच्या फार मोठ्या संग्रहाचा उपयोग करते. तिचा आवाका आणि मर्यादा अजून स्पष्ट झाल्या नाहीत, परंतु जुळ्या मूळ संख्या अनंत आहेत का नाहीत ह्यासारखे अनुत्तरित प्रश्न सोडवायला मानवी बुद्धिमत्तेचीच गरज लागेल, यांत्रिक बुद्धी अपुरी ठरेल असे म्हटल्याशिवाय राहवत नाही.

गणितातील निगमन पद्धती

बऱ्याच जणांचा समज असतो की, गणित म्हणजे आकडेमोड! पण आकडेमोड हा गणिताचा अगदी लहानसा भाग आहे. अगदी वेगवेगळ्या प्रकारच्या संरचना गणितामध्ये निर्माण केल्या जातात. त्यांपैकी काही दोन बिंदूंमधील अंतराशी संबंधित (distance structures) असतात, काही बेरीज-गुणाकार अशा बैजिक क्रियांशी संबंधित (algebraic structures) असतात, व इतरही अनेक धर्तीच्या असतात. ज्या विशिष्ट रीतीने या संरचनांची उभारणी केली जाते, आणि त्यांमधील संबंध शोधले जातात तिला निगमन पद्धती (deductive method) असे म्हणतात. थोडक्यात सांगायचे झाले तर, गृहीत धरलेल्या गोष्टी प्रथमत: स्पष्टपणे सांगायच्या, त्यांना गृहीतके (hypotheses) असे म्हणायचे. त्या गोष्टी बाह्य जगाशी जुळल्याच पाहिजेत असे काही नाही. उदाहरणार्थ, ‘एक सरळ रेषा व तिच्यावर नसणारा एक बिंदू दिला असल्यास त्या बिंदूतून जाणारी आणि त्या रेषेला समांतर असणारी एकच सरळ रेषा असते’ हे युक्लिडच्या भूमितीचे एक गृहीतक आहे. त्याचप्रमाणे ‘एक सरळ रेषा व तिच्यावर नसणारा एक बिंदू दिला असल्यास त्या बिंदूतून जाणारी आणि त्या रेषेला समांतर असणारी एकही सरळ रेषा नसते’ हे देखील कुणाचे गृहीतक असू शकते. वस्तुतः रीमानच्या विवृत्तीय भूमितीचे (Elliptic Geometry of Riemann) एक गृहीतक हेच आहे. एकापेक्षा अधिक गृहीतके असली तर त्यांच्यात अंतर्विरोध (internal contradiction) असता कामा नये एवढे पाळावे लागते. यानंतर गृहीतकांपासून ज्या ज्या गोष्टी तर्कशुद्ध रीतीने निष्पन्न होऊ शकतात, त्या पायरीपायरीने (step by step) मांडत जायचे. या निष्पन्न झालेल्या गोष्टींना प्रमेय किंवा सिद्धांत (theorem) असे म्हणतात, आणि त्यांच्यासाठी दिलेल्या युक्तिवादाला सिद्धता (proof) असे म्हणतात. खूपशा गणितज्ञांना कॉफी प्यायला आवडते. तिचे घुटके घेता घेता त्यांची तंद्री लागते आणि काही वेळा त्यांना एकदम नवा सिद्धांत सुचतो असे अनेक वेळा झाले आहे; म्हणून कुणी तरी गमतीने ‘कॉफीचे सिद्धांतात रूपांतर करणारे यंत्र’ अशी गणितज्ञाची ओळख सांगितली आहे!

जोपर्यंत आपण आपली गृहीतके बदलत नाही तोपर्यंत ती वापरून सिद्ध केलेल्या प्रमेयांची सत्यता त्रिकालाबाधित असते, ती कुणा व्यक्तीवर अवलंबून नसते; त्यांच्याबाबत केव्हाही, कुणाचाही मतभेद असू शकत नाही. गणिताचा हा गाभा आहे, आणि गणिताचे हे व्यवच्छेदक लक्षणही आहे. इथे कुणाचे काही मत कुणाला मान्य आहे की नाही अशा वादाला वावच नाही. गणिताखेरीज इतर शास्त्रात, म्हणजे पदार्थविज्ञान, रसायन, जीव अशा शास्त्रांत, वेगळ्या रीतीने काम केले जाते. त्या रीतीला विगमन पद्धती (inductive method) असे म्हणतात. सृष्टीमध्ये सूक्ष्म निरीक्षणे (observations) करायची, त्यांच्यावर आधारलेले काही अंदाज बांधायचे, शक्य असेल तर प्रयोगशाळेमध्ये त्यांचा पडताळा घेऊन बघायचा, आणि मग ते एका उपपत्तीच्या (theory) स्वरूपात मांडायचे. जोपर्यंत त्या उपपत्तीने वर्तवलेली भाकिते खरी ठरतात आणि नवीन प्रतिलापी (contradictory) निरीक्षणे मिळत नाहीत, तोपर्यंत ती उपपत्ती स्वीकारली जाते. आइन्स्टाइनच्या सामान्य सापेक्षता उपपत्तीबाबत (General Relativity Theory) असेच झाले आहे. उलटपक्षी, मांडलेल्या उपपत्तीत फेरबदल करावा लागतो किंवा ती सोडूनच द्यावी लागते, जसे पदार्थविज्ञानातील महास्फोट उपपत्ती (Big Bang Theory) पुढे आल्यामुळे स्थिरस्थिती उपपत्ती (Steady State Theory) सोडून द्यावी लागत आहे. कुठल्याही गणिती प्रमेयाला मात्र असा डच्चू कधी मिळत नाही.

गणिती संरचनेचे आदिम उदाहरण म्हणजे युक्लिड याने ‘मूलतत्त्वे’ (Elements) नावाच्या तेरा खंडांच्या ग्रंथात विकसित केलेली भूमिती. पाच गृहीतकांनी सुरुवात करून त्याने किती तरी सिद्धांत आणि त्यांच्या सिद्धतांचा केवढा मोठा प्रपंच मांडला आहे. सिद्धता हा शब्द ऐकला की बऱ्याच जणांच्या अंगावर काटा उभा राहतो. याचे कारण खूपदा ती क्लिष्टपणे दिलेली असते. पण सिद्धता जितकी सोपी तितकी ती उत्कृष्ट. सातवीच्या बालभारती पुस्तकामध्ये दिलेले पायथागोरसचे प्रमेय असे आहे : काटकोन त्रिकोणातील कर्णाच्या लांबीचा वर्ग हा इतर दोन बाजूंच्या लांबींच्या वर्गांच्या बेरजेइतका असतो. हीच गोष्ट चिह्ने वापरून सांगायची झाली, तर कर्णाची लांबी c असेल व इतर दोन बाजू a आणि b लांबीच्या असतील तर c² = a² + b² असे सूत्र मिळाले पाहिजे. हे दाखवून द्यायचे असल्यास काटकोन त्रिकोणाच्या कर्णावर काढलेल्या चौरसाचे क्षेत्रफळ त्या त्रिकोणाच्या दोन बाजूंवर काढलेल्या चौरसांच्या क्षेत्रफळांच्या बेरजेइतके असते असे दाखवले की काम झाले. याची चित्रमय सिद्धता अशी आहे –

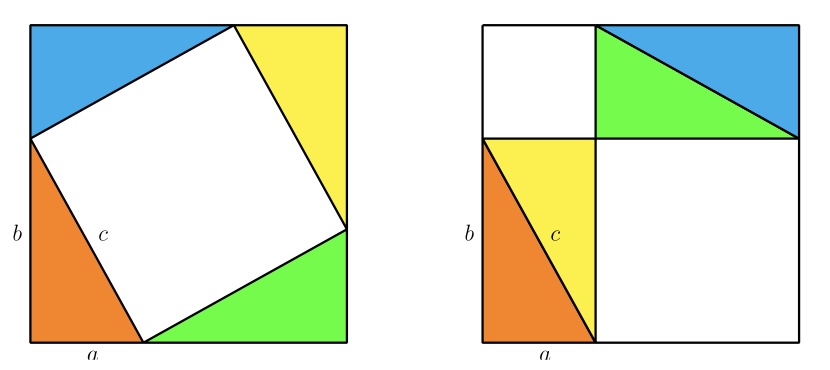
वरील दोनही आकृतीत a + b लांबी-रुंदी असलेले सारख्याच आकाराचे चौरस काढलेले आहेत. दोन्ही आकृत्यांत दिलेल्या आकाराचे चार रंगीत काटकोन त्रिकोण आहेत; फक्त त्यांची रचना वेगळ्या प्रकारे केली आहे इतकेच. हे चार काटकोन त्रिकोण गाळून टाकले तर पहिल्या आकृतीत एकच चौरस उरतो; त्याची लांबी-रुंदी c आहे व म्हणून त्याचे क्षेत्रफळ c² आहे. दुसऱ्या आकृतीत मात्र दोन चौरस उरतात; त्यांतील एकाची लांबी-रुंदी a आहे आणि म्हणून त्याचे क्षेत्रफळ a² आहे, तर दुसऱ्याची लांबी-रुंदी b आहे आणि म्हणून त्याचे क्षेत्रफळ b² आहे. आता उघड आहे की पहिल्या आकृतीत उरलेल्या चौरसाचे क्षेत्रफळ दुसऱ्या आकृतीत उरलेल्या दोन चौरसांच्या क्षेत्रफळांच्या बेरजेइतके असणार, म्हणजेच c² = a² + b² . खेळ खलास, सिद्धता संपली!

गणित शिकण्या-शिकवण्याच्या दोन पद्धती

प्राथमिक स्वरूपाचे गणित शिकवण्याच्या आणि शिकण्याच्या दोन भिन्न पद्धती आहेत. एक आहे गणनविधीचा वापरणारी (algorithmic) व दुसरी आहे स्वतःला विचार करायला लावणारी. दोन्हींमध्ये काही इष्ट आणि काही अनिष्ट बाबी आहेत. पहिल्या पद्धतीत विचार करण्याचा मक्ता आपण दुसऱ्या कुणाला दिला असतो. त्या व्यक्तीने घालून दिलेला पायंडा आपण पाळत जातो. उदाहरणार्थ, काळ-काम-वेगाची त्रैराशिके किंवा पंचराशिके सोडवताना आपण अंशात (numerator) आणि छेदात (denominator) ठरावीक राशी पटकन लिहून टाकतो आणि उत्तर काढतो. तसेच द्विघाती समीकरणाच्या (quadratic equation) उकली मिळवण्याचे सूत्र वापरून दोन उत्तरे लगेच मिळवतो. त्यामुळे वेळ व श्रम वाचतात हे खरे, परंतु यात धोका असा आहे की ठरवून दिलेला गणनविधी तंतोतंत जसाचा तसा आठवला नाही किंवा आपण तो बिनचूक लिहिला नाही, तर सगळेच मुसळ केरात जाते. आम्ही शाळेत असताना तीसपर्यंतचे पाढे पाठ करायला लावत, तो यातलाच प्रकार आहे. पाढे पाठ असतील व एकोणतीस साते तिहोत्रीदोन, म्हणजे 29 X 7 = 203 असे लिहिले तर उत्तम, नाहीतर पंचाईत. पण 29चा पाढा पाठ नसला तरी थोडा विचार करून 29 X 7 = (20 + 9) 7 = 140 + 63 = 203 हे उत्तर आपण मिळवू शकतो. या पुढे जाऊन ax² + bx + c = 0 या द्विघाती समीकरणाच्या [— b ± √( b² — 4ac)] / 2a या दोन उकली लक्षात ठेवायला काही सोप्या नाहीत. पण x² + 4x + 1 = 0 हे समीकरण सोडवायचे असेल, तर x² + 4x या पहिल्या दोन पदांचा पूर्ण वर्ग करायचा असतो एवढे ध्यानात ठेवले व x² + 4x + 1 = (x + 2)² — 4 + 1 = (x + 2)² — 3 असे लिहिले तर आपल्याला x = — 2 + √3 आणि x = — 2 — √3 या उकली सहज मिळून जातात. शिकण्या-शिकवण्याच्या या दुसऱ्या पद्धतीमध्ये पाठांतरावर व स्मरणशक्तीवर भर कमी असतो, पण स्वतःचे डोके लढवायला वाव असतो, गणित सोडवण्याच्या रितीमागील विचारधारा समजून घेतली जाते.

आता या दोन पद्धतींपैकी कोणती अवलंबावी? मी माझ्या मुलींबाबत दोन्ही पद्धतींचे प्रयोग केले आहेत. खरे म्हणजे या प्रश्नाचे उत्तर शिक्षकाची समजावून सांगण्याची कुवत आणि विद्यार्थ्याची समजून घेण्याची ताकद या दोन्ही गोष्टींवर अवलंबून आहे. या शक्ती जितक्या जास्त असतील तितकी दुसरी म्हणजे स्वतःला विचार करायला लावणारी पद्धतच वापरणे श्रेयस्कर आहे. सुरुवातीच्या काही वर्षांत गणनविधी वापरून काम आटोपते घेणे स्वाभाविक आहे, पण तीच सवय कायमची न लागलेली बरी. जरी वेळ व श्रम अधिक लागले, तरी तर्कशुद्ध विचार करण्याच्या प्रवृत्तीला बढावा दिलेला बरा, कारण तर्कशुद्ध विचार हा गणिताचा मानबिंदू आहे. शिवाय एखाद्या गणनविधीमागची कारणमीमांसा माहीत असली तर तो गणनविधी लक्षात राहणे सोपे असते, आणि जितका विचारशक्तीचा भाग जास्त तितका लांबचा पल्ला गाठता येतो, खोलवर जाता येते.

गणिताची नावड कशी घालवता येईल?

शालेय जीवनापासूनच कित्येक जणांचे गणित कच्चे राहून जाते व त्यात आवड निर्माण होऊ शकत नाही, याला बरीच कारणे असू शकतात. गणिताचा शिक्षक कुठली तरी एक पद्धत वापरून सर्व वर्गाला शिकवतो. परंतु ती पद्धत वर्गातील काही जणांच्या पचनी पडते, तर बाकीच्यांना ती सोसत नाही. उदाहरणार्थ, ज्यांना घोकंपट्टी करायचा अतिशय कंटाळा असतो, त्यांना गणनविधीच्या पद्धतीत मुळीच स्वारस्य वाटत नाही. उलटपक्षी, ज्यांची आकलनशक्ती बेताची आहे, त्यांच्यासाठी पाठांतर हाच तरणोपाय असतो. म्हणून ‘सब घोडे बारा टक्के’ असे मानून चालणार नाही. हीच गोष्ट शिक्षकांच्या बाबतीतही खरी आहे. सगळ्या शिक्षकांना फक्त गणनविधीच वापरून शिकवायला सांगितले तर मातब्बर शिक्षकांचा शिकवण्यातील आनंद हिरावून घेतला जाईल. उलट, ज्या शिक्षकांना सूक्ष्म विचार स्पष्ट करून समजावणे जड जाते त्यांनी पठडीतूनच शिकवणे चांगले. पण पुढचा प्रश्न असा की गुरू-शिष्यांच्या कुवतीचा मेळ घालायचा कसा? आपल्या शिक्षणप्रणालीत वैयक्तिक लक्ष देता येणे शक्य असेल, तर शिक्षकांचे व विद्यार्थ्यांचे काही विभाग पाडून इष्टतम (optimal) परिणाम मिळवता येतील, एवढेच म्हणता येईल.

शिक्षक सांगतील ते ऐकून घ्यायचे आणि त्याप्रमाणे आपल्या वहीत उदाहरणे, उपप्रमेये सोडवायची असे गणिताच्या तासाला कायम चाललेले असते. इतर शास्त्रांच्या तासांना जसे कधी कधी प्रयोगशाळेत जायला मिळते किंवा इतिहास-भूगोलाच्या तासांना केव्हा केव्हा अवांतर गप्पा ऐकायला मिळतात तसे गणिताच्या बाबतीत फारसे कधी होत नाही. मग मुलांना निरुत्साह येणारच. तो घालवायचा असेल तर कागदावर आकृती काढून व कातरकाम करून काही प्रतिकृती बनवल्या, ओरिगामीसारख्या छंदाची ओळख करून दिली तर चैतन्य निश्चित येऊ शकते. भूमिती आणि हस्तव्यवसाय यांची सांगड घालणे उपकारक ठरू शकते.

गणित या विषयाला मुले भिऊन असण्याचे एक कारण त्याच्याच स्वरूपात दडलेले आहे. एखादे गणित बरोबर आले की संपूर्ण गुण मिळतात, 10 पैकी 10 किंवा 1 पैकी 1. पण ते गणित चुकले तर खाडकन 0 गुण दिले जातात, म्हणजे खाशील तर तुपाशी नाहीतर उपाशी असा प्रकार झाला. शिवाय एखादे गणित चुकायला फार काही लागत नाही, कुठल्याही एका पायरीवर थोडीशी हयगय झाली की सगळेच बिनसते. यामुळे गणितातील प्रश्नाचे उत्तर मिळाल्यावरही आपल्याला धास्ती असते. मात्र सध्याच्या जमान्यात गणितातही अंशतः गुण द्यायला सुरुवात झाल्याने परिस्थिती सुधारत आहे.

एक प्रश्न सतत चर्चिला जातो तो असा की, गणितापासून खूप जण फटकून का राहत असावेत, तिकडे ढुंकूनही का बघत नसावेत? याचे एक निराळेच कारण मनात येते. गणितातील नैपुण्याला समाजात शिरोधार्य मानले जाते. हा एकप्रकारे गणिताचा उदोउदोच म्हटला पाहिजे. त्यामुळे गणित हा फक्त हुशार लोकांचाच प्रांत आहे अशी समजूत होऊन जाते. म्हणून गणिताच्या वाटेलाच जाऊ नये असे अनेकांना वाटणे साहजिक आहे. परिणामी, बौद्धिकदृष्ट्या समर्थ असलेले कितीतरी लोक गणिती विचाराला वंचित होतात. यावर प्रमुख उपाय म्हणजे गणिताला देव्हाऱ्यातून बाहेर काढणे आणि इतर उत्तमोत्तम विषयांच्या पंक्तीला आणून बसवणे. इतर विषयांत प्रावीण्य मिळवायला हुशारी लागतेच; ती जरा वेगळ्या धर्तीची असते इतकेच. तसे बघितले तर गणितात काम करणारे सगळेच काही रामानुजन नसतात. तरीही ते आपापल्या परीने चांगले काम करत असतात, जिद्दीने, चिकाटीने. त्यांपैकी बरेचसे शाळा-कॉलेजात चमकलेले नसतातही. गणित या विषयाला हस्तिदंती मनोऱ्यात न ठेवल्याने गणित्यांना जनमानसात आपुलकीचे स्थान मिळावे एवढाच माझा हेतू आहे हे सगळे लिहिण्यामागे.

समाजजीवनातील गणिताचे स्थान

प्राथमिक गणितापासून प्रगत गणितापर्यंत सर्व प्रकारचे गणित आपल्या दैनंदिन व्यवहारात कसे व किती पसरून राहिले आहे हे सांगण्याची गरज नाही. पूर्वी उच्च शिक्षणापैकी भौतिकी आणि अभियांत्रिकी शाखांत गणिताचे उपयोजन मोठ्या प्रमाणावर होई, पण आता जीवशास्त्र आणि समाजविज्ञान यांच्या काही भागात गणित व सांख्यिकी (statistics) यांचा शिरकाव झाला आहे. या व्यापकतेचे कारण असे आहे की, गणिताची मुळे खूप खोलवर गेलेली आहेत. दुसरे असे की गणितातला तर्कशुद्ध विचार सामाजिक आरोग्याला फार उपकारक असतो. उदाहरणार्थ, श्रद्धा आणि अंधश्रद्धा कोणत्या गृहीतकांवर आधारलेल्या आहेत याचा शोध घेतला, ती गृहीतके स्वीकारण्यासारखी आहेत का व त्यांची परिणती निश्चितपणे कशात होते हे गणिती म्हणजे तार्किक पद्धतीने स्पष्ट झाले, तर कित्येक वाद विकोपाला जाणार नाहीत. थोडक्यात, घटनांचा कार्यकारणभाव लक्षात घेता आला तर वितंडवाद टळतील. गणितज्ञ मंगला नारळीकर यांना 1986 साली कर्करोग झाला असता घरातल्या कुणीतरी लघुरुद्राची पूजा करावी असे सुचवले, तेव्हा त्यांनी नकार दिला. आपल्यावर घोर आपत्ती आली असतानाही अप्रमाणित उपायांच्या आहारी जायचे नाही हे गणिताच्या तर्कशुद्धतेनेच त्यांच्या अंगी बाणवले होते. काही जण मात्र गणितात निष्णात असूनही अंकभाकितासारख्या (numerology) अगणिती गोष्टींचा पाठपुरावा करताना दिसतात. समर्थ रामदासांनी दासबोधात सांगितलेली पढतमूर्खाची लक्षणे त्यांना लागू पडावीत.

(या लेखाची संक्षिप्त आवृत्ती 'साप्ताहिक साधना'च्या बालकुमार २०२३ या दिवाळी अंकात प्रकाशित झाली होती, बालकुमार आणि त्यांचे पालक, शिक्षक यांच्यासाठी. लेखातील चित्रे गिरीश सहस्रबुद्धे यांनी ‘साप्ताहिक साधना’साठी काढली होती. लेख व चित्रे प्रकाशित करण्यासाठी ‘साप्ताहिक साधना’चे सहकार्य लाभले. त्यांचे आभार.)
– – –
बालमोहन लिमये

(balmohan.limaye@gmail.com)



लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.

बालमोहन लिमये यांचे इतर लिखाण