सममित आकृतींचा शोध - भाग २
सममित आकृतींचा शोध
बालमोहन लिमये
भाग २
कागदावर काढता येणाऱ्या, म्हणजे प्रतलावर (plane) सापडणाऱ्या, बहुभुज (polygon) चित्राकृतींपैकी एखादा बहुभुज पूर्णतः सममित (symmetric) हवा असला तर त्या बहुभुजाच्या सर्व बाजू समान लांबीच्या असाव्या लागतात व त्याचे सर्व कोन समान असावे लागतात. अशा बहुभुजाला सुसम बहुभुज (regular polygon) असे म्हणतात. जर p हा दोनपेक्षा मोठा कोणताही पूर्णांक असेल, तर p बाजू असलेला सुसम बहुभुज सहज काढता येतो हे आपण भाग १मध्ये पाहिले. अवकाशात (space) सापडणाऱ्या घनाकृतींपैकी एखादा बहुफलक (polyhedron) पूर्णतः सममित हवा असला तर त्याचे सर्व फलक (faces) सुसम बहुभुज तर असलेच पाहिजेत; शिवाय त्या सगळ्यांच्या बाजूंची संख्या समान असली पाहिजे, आणि त्या बहुफलकाच्या प्रत्येक शिरोबिंदूपाशी येऊन मिळणाऱ्या फलकांची संख्या समान असली पाहिजे. अशा बहुफलकाला सुसम बहुफलक (regular polyhedron) असे म्हणतात. भाग १मध्ये बराच प्रयत्न करून 4, 6, 8 फलक असलेले सुसम बहुफलक कसे मिळवता येतात हे आपण पाहिले. या घनाकृती खाली दाखवल्या आहेत.
|

|

|
या तिन्ही सुसम बहुफलकांचे फलक त्रिकोणी किंवा चौकोनी आहेत, व त्यांच्या शिरोबिंदूंपाशी तीन किंवा चार फलक येऊन मिळतात. सुसम बहुफलकांचे फलक पंचकोनी, षट्कोनी वगैरे असू शकतील का आणि त्यांच्या शिरोबिंदूंपाशी पाच, सहा वगैरे फलक येऊन मिळू शकतात का असे प्रश्न सहजच मनात येतात. हे प्रश्न सोडवण्यासाठी आपल्याला अनंत शक्यता लक्षात घ्याव्या लागतील. पण असे चाचपडत बसण्याऐवजी आपण उलट्या दिशेने हे प्रश्न हाताळू या, म्हणजे एखादा बहुफलक सुसम असला तर त्याच्या फलकसंख्येवर काय निर्बंध आपोआप पडतात ते जाणून घेऊ या.
श्लेफ्ली चिह्न
कोणत्याही सुसम बहुफलकाबाबत दोन संख्या महत्त्वपूर्ण आहेत. एक म्हणजे त्याच्या प्रत्येक फलकाच्या बाजूंची संख्या p, व दुसरी म्हणजे त्याच्या प्रत्येक शिरोबिंदूपाशी येऊन मिळणाऱ्या फलकांची संख्या q. मग त्या सुसम बहुफलकाचा निर्देश {p, q} असा करता येईल. लुड्विग श्लेफ्ली (Ludwig Schläfli) या स्विस गणितज्ञाने एकोणिसाव्या शतकात प्रथम प्रस्तुत केलेल्या या निर्देशाचे श्लेफ्ली चिह्न (Schläfli symbol) हे नाव आजही प्रचलित आहे. त्यातील p, q या संख्यांभोवतीचे महिरपी कंस त्या संख्यांनी होणारा संच (set) दाखवत नाहीत, तर एक क्रमित जोडी (ordered pair) दाखवतात. यानुसार सुसम चतुष्फलकाचे श्लेफ्ली चिह्न ठरते {3, 3}, सुसम षट्फलकाचे श्लेफ्ली चिह्न ठरते {4, 3}, व सुसम अष्टफलकाचे श्लेफ्ली चिह्न ठरते {3, 4}. आता सुसम बहुफलकांसाठी अशी कोणकोणती श्लेफ्ली चिह्ने संभवतात ते शोधू या. आपण फक्त बहिर्वक्र (convex) बहुफलकांचाच विचार करणार आहोत ही गोष्ट लक्षात असू द्या.
समजा {p, q} हे श्लेफ्ली चिह्न असलेला एक सुसम बहुफलक अस्तित्वात आहे. मग त्याचा प्रत्येक फलक p बाजूंचा सुसम बहुभुज असणार; तसेच त्या बहुफलकाच्या प्रत्येक शिरोबिंदूपाशी q फलक येऊन मिळणार व एक घन कोन (solid angle) तयार करणार. कुठल्याही बहुभुजाला निदान तीन तरी बाजू असल्या पाहिजेत म्हणून p हा पूर्णांक किमान 3 असला पाहिजे, आणि कुठल्याही बहुफलकाच्या शिरोबिंदूपाशी घन कोन तयार होण्यासाठी निदान तीन तरी फलक येऊन मिळाले पाहिजेत, म्हणून q हा पूर्णांकदेखील किमान 3 असला पाहिजे.
सुसम p-भुजाचा प्रत्येक आंतरकोन (p – 2)π/p रेडिअनचा असतो हे आपण भाग १मध्ये पाहिले आहे. (येथे π ही 3.14 च्या जवळपासची एक विशिष्ट संख्या आहे, आणि 2π रेडिअन = 360 अंश.) प्रत्येक शिरोबिंदूपाशी असे q फलककोन होतात, व म्हणून त्या सर्वांची बेरीज होते (p – 2)qπ/p. युक्लिडने बहिर्वक्र बहुफलकांबाबत केलेल्या विधानानुसार ही बेरीज 2π रेडिअनपेक्षा कमी असली पाहिजे; याचा अर्थ असा की (p – 2)qπ/p < 2π ही असमानता (inequality) पाळली पाहिजे. तिच्या दोन्ही बाजूंना π या संख्येने भागले व p या संख्येने गुणले तर ती (p – 2)q < 2p, म्हणजेच pq < 2p + 2q, किंवा
(p – 2)(q – 2) < 4
अशी होते. ही असमानता (inequality) उरलेल्या सगळ्या युक्तिवादाचा गाभा आहे. आता p आणि q हे पूर्णांक किमान 3 असले पाहिजेत, व त्यामुळे s = (p – 2)(q – 2) हा पूर्णांक 1, 2, 3 यांपैकीच असू शकतो. आता उघड आहे की जर s = 1 असेल, तर p = 3 व q = 3 असले पाहिजेत; जर s = 2 असेल तर p = 4 व q = 3 किंवा p = 3 व q = 4 असले पाहिजेत, आणि जर s = 3 असेल तर p = 5 व q = 3 किंवा p = 3 व q = 5 असले पाहिजेत. याचा अर्थ p व q यांच्या इतर कुठल्याही किंमती (p – 2)(q – 2) < 4 ही असमानता पाळत नाहीत. उदाहरणार्थ, p = 4 व q = 4 या किंमतींसाठी (p – 2)(q – 2) = (4 – 2)( 4 – 2) = 2 गुणिले 2 = 4; तसेच p = 6 व q = 3 या किंमतींसाठी (p – 2)(q – 2) = (6 – 2)( 3 – 2) = 4 गुणिले 1 = 4. पण 4 ही संख्या 4 याच संख्येपेक्षा काही कमी नाही, व म्हणून वरील असमानता पाळली जात नाही. याप्रमाणे खाली दिलेल्या कोष्टकातील केवळ पाच शक्यता पुढे येतात.
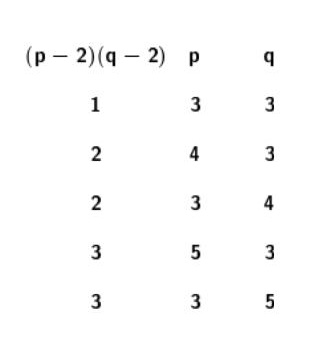
याचा अर्थ असा होतो की सुसम बहुफलकाच्या शिरोबिंदूपाशी 3, 4, किंवा 5 समभुज त्रिकोण (p=3) एकत्र येऊ शकतात, 3 चौरस (p=4) एकत्र येऊ शकतात, अथवा 3 सुसम पंचकोन (p=5) एकत्र येऊ शकतात; यांखेरीज इतर कोणतेही सुसम बहुभुज एकत्र येऊ शकत नाहीत. उदाहरणार्थ, 4 चौरस एकत्र येऊ शकत नाहीत किंवा 3 सुसम षट्कोन एकत्र येऊ शकत नाहीत. वरील कोष्टकातील पहिल्या तीन शक्यता आपण सुसम चतुष्फलक, सुसम षट्फलक व सुसम अष्टफलक यांच्या रूपात प्रत्यक्षात आणून दाखवल्या आहेत. राहता राहिल्या शेवटच्या दोन शक्यता, म्हणजे प्रत्येक शिरोबिंदूपाशी तीन सुसम पंचकोन येऊन मिळतील अशी घनाकृती आणि प्रत्येक शिरोबिंदूपाशी पाच समभुज त्रिकोण येऊन मिळतील अशी घनाकृती. या दोन घनाकृती असू शकतात की नाही हे ठरवले म्हणजे प्रश्न मिटला. आपण केलेल्या या विश्लेषणामुळे अनंत उत्तरे संभवत असलेले आपले गहन प्रश्न आवाक्यात आल्यासारखे झाले आहेत. तरीही हे उरलेले काम काही सोपे नाही.
द्वादशफलक व विंशतिफलक
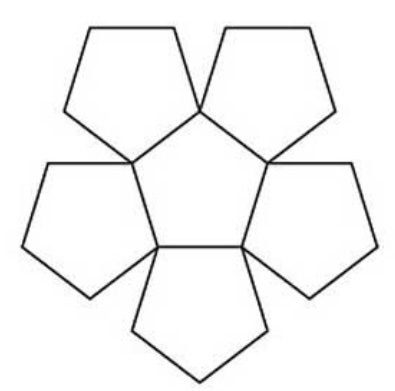
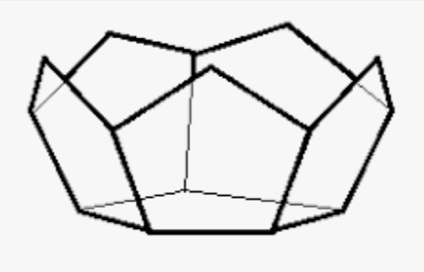
आपल्या आधीच्या अनुभवानुसार कागदावर एक सुसम पंचकोन काढून त्याच्या प्रत्येक बाजूवर त्याच आकाराचा सुसम पंचकोन उभारू या. आता ही आकृती कापून काढली व प्रथम काढलेल्या सुसम पंचकोनाच्या पाचही बाजू मुडपून नंतर काढलेले पाच पंचकोन वर उचलले आणि जवळजवळच्या (समान लांबीच्या) बाजू जोडून टाकल्या की आपल्याला एक वाडगा (bowl) मिळतो. ही कृती खालील चित्रात डावीकडे व मध्यभागी दाखवली आहे.
|
|
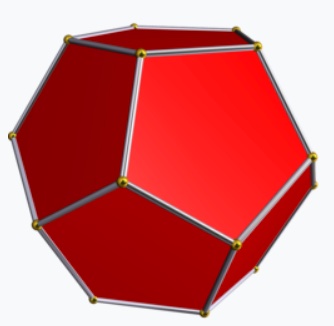
|
या वाडग्याला सहा पंचकोनी फलक असतात व त्याच्या मोकळ्या कडांचा एक वितलीय दशभुज (skew decagon) बनतो. असाच आणखी एक वाडगा बनवून या दोन वाडग्यांच्या कडांनी बनलेले दशभुज एकमेकांवर बसवले की आपल्याला बारा फलकांची बंदिस्त घनाकृती म्हणजे एक द्वादशफलक (dodecahedron) मिळतो. त्याचा प्रत्येक फलक सुसम पंचकोन असतो व त्याच्या प्रत्येक शिरोबिंदूपाशी तीन फलक येऊन मिळतात, म्हणून तो सुसम बहुफलक आहे. त्याचे श्लेफ्ली चिह्न आहे {5, 3}. ही घनाकृती वरील चित्रात उजवीकडे दाखवली आहे.
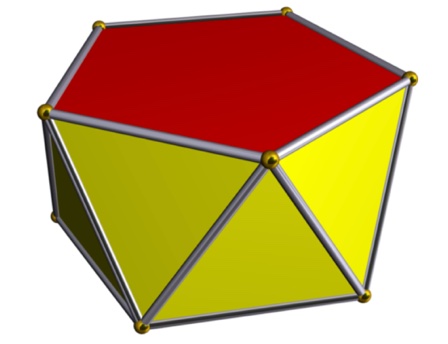
शेवटी आपल्याला पाच त्रिकोण प्रत्येक शिरोबिंदूपाशी एकत्र येऊन मिळणारी घनाकृती शोधायची आहे. त्यासाठी प्रथम दोन सारख्या आकाराचे सुसम पंचकोन एकावर एक काही अंतर ठेऊन समांतर धरायचे व ते एकमेकांना त्यांच्या कोपऱ्यांनी असे जोडायचे की एकाआड एक त्रिकोणांची पट्टी (alternating band of triangles) तयार होईल. दोन समांतर पंचकानांमधील अंतर असे निवडायचे की हे सगळे दहा त्रिकोण समभुज होतील. या घनाकृतीला पंचकोनी प्रतिकोनचिती (pentagonal antiprism) असे नाव आहे. ती खालील चित्रात डावीकडे दाखवली आहे.
|

|
|
या घनाकृतीचे दोन फलक पंचकोनी तर दहा फलक त्रिकोणी आहेत आणि तिच्या प्रत्येक शिरोबिंदूपाशी तीन त्रिकोण व एक पंचकोन असे चार फलक येऊन मिळतात. पण आपल्याला पंचकोनी फलक तर नको आहेत. म्हणून ते काढून टाकून दोन्ही पंचकोनी पायथ्यांवर एकेक मेरू (pyramid) बसवायचा; त्यांची शिखाग्रे अशा अंतरावर ठेवायची की त्यांना पायथ्यांशी जोडणारे त्रिकोण समभुज होतील. ही कृती वरील चित्रात मध्यभागी व उजवीकडे दाखवली आहे. अशाप्रकारे आपल्याला दहा अधिक पाच अधिक पाच अशा एकूण वीस फलकांची बंदिस्त घनाकृती म्हणजे एक विंशतिफलक (icosahedron) मिळतो. त्याचा प्रत्येक फलक समभुज त्रिकोण असतो व त्याच्या प्रत्येक शिरोबिंदूपाशी पाच फलक येऊन मिळतात, म्हणून तो सुसम बहुफलक आहे. त्याचे श्लेफ्ली चिह्न आहे {3, 5}.
प्लेटोच्या पाच घनाकृती
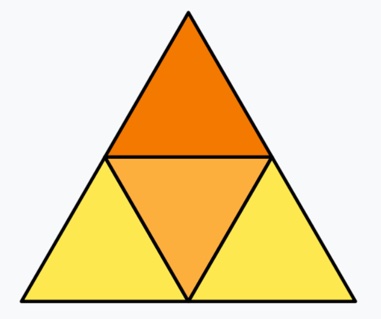
अशा प्रकारे आपण सुसम बहुफलकांच्या पाचही शक्यता प्रत्यक्षात आणून दाखवल्या आहेत. सुसम बहुफलकाचे वस्तुरूप (model) बनवायचे असेल तर कडक कागदावर किंवा पातळ पुठ्ठ्यावर ठरावीक सुसम बहुभुजांच्या आकृती एकमेकांच्या बाजूंना लागून काढायच्या. सामाईक बाजूंवर घड्या घालून त्या बहुभुजांचे फलक बनवायचे व ते योग्य कडांवर चिकटवायचे. अशा कागदावरील मांडणीला त्या बहुफलकाचे जाल (net) असे म्हणतात. आपण शोधलेल्या प्रत्येक सुसम बहुफलकाचे जाल खाली दाखवले आहे.
|

|
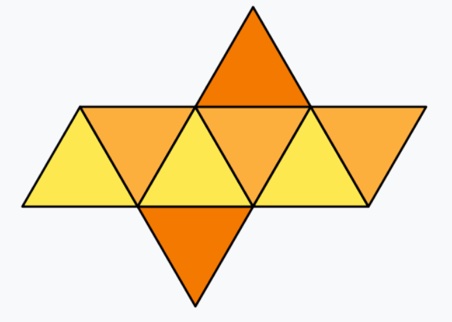
|
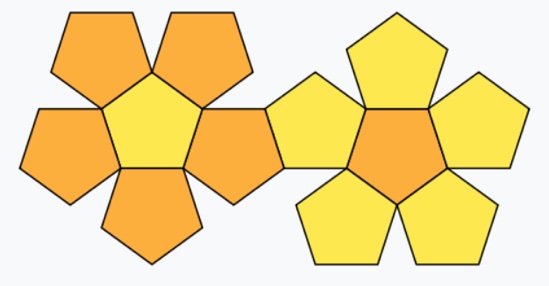
|

|
सुसम द्वादशफलक आणि सुसम विंशतिफलक यांचा शोध अनपेक्षितच म्हटला पाहिजे. उच्चतर मितींमधील पूर्णतः सममित आकृतींचा साकल्याने विचार करताना हे दोन बहुफलक तीन मितींच्या सुसम घनाकृतींमध्ये उपटसुंभासारखे घुसून आलेले वाटतात. ग्रीक गणितज्ञांना सुरूवातीपासून ते परिचित होते हे मात्र विशेष आहे. गणित, पदार्थविज्ञान व तत्त्वज्ञान यांमध्ये जाणकार असणाऱ्या हरमान वाइल (Hermann Weyl) यांनी आपल्या ‘सममिति’ (Symmetry) या छोटेखानी पण उत्कृष्ट पुस्तकात म्हटले आहे की या दोन सुसम बहुफलकांचा शोध गणिताच्या इतिहासातील सर्वात सुंदर व संविशेष (singular) शोधांत गणला पाहिजे. सुसम बहुफलक फक्त पाचच असतात याची पहिली गणिती सिद्धता देण्याचे श्रेय ग्रीक तत्त्ववेत्ता प्लेटो (Plato) याचा शिष्योत्तम थिइटीटस (Theaetetus, 417-369 BCE) याला मिळते. प्लेटोने आपल्या `टिमेअस’ (Timaeus) नावाच्या प्रसिद्ध संवादात या पाच बहुफलकांचे विवेचन केले असल्यामुळे नंतरच्या काळात हे पाच सुसम बहुफलक ‘प्लेटोच्या घनाकृती’ (Platonic Solids) म्हणून नावारूपाला आले.
आपण शाळेत आणि महाविद्यालयात शिकतो ती भूमिती युक्लिड या ग्रीक गणितज्ञाने इसवी सनापूर्वी सुमारे तीनशे वर्षे लिहिलेल्या ‘मूलतत्त्वे’ (Elements) या ग्रंथावर आधारलेली आहे. युक्लिडने ग्रीक पूर्वसुरींनी मिळवलेले गणिती ज्ञान सुसूत्रपणे एकत्र करून व त्यात भर घालून आपला ग्रंथ लिहिला. त्याचे एकूण तेरा भाग आहेत. पहिल्या भागात अगदी प्राथमिक चर्चेने सुरुवात केली आहे, पण नंतर भूमितीच्या सखोल प्रमेयांची आणि रचनांची तर्कशुद्ध मांडणी निगमन पद्धतीने (Deductive method) केली आहे. शेवटच्या भागातील अखेरच्या काही विधानांत पाच सुसम घनाकृतींपैकी प्रत्येकीची रचना एका गोलात (sphere) करून दाखवली आहे, पुढील क्रमाने : चतुष्फलक, अष्टफलक, षट्फलक, विंशतिफलक, द्वादशफलक. युक्लिडच्या रचनांवरून समजून येते की पाचही सुसम घनाकृती एकगोलीय (conspheric) असतात, जसे सगळे सुसम बहुभुज एकचक्रीय (concyclic) असतात. ग्रंथाच्या अगदी अखेरीस युक्लिडने ‘आता मी म्हणतो की या पाच घनाकृतींखेरीज इतर कोणतीही घनाकृती समकोनी व समभुज फलकांनी अंतर्भूत करता येत नाही’ असे जणू विजयोद्गार काढले आहेत. तेरा भागांचा इतका विस्तृत ग्रंथ लिहिण्यामागचा युक्लिडचा अंतिम हेतू सुसम घनाकृती नेमक्या कोणत्या हे प्रस्थापित करायचा होता असे काही इतिहासज्ञांचे म्हणणे आहे.
इथे एका बारकाव्याचा उल्लेख करणे जरूर आहे. सममित घनाकृतीच्या शिरोबिंदूपाशी होणारा आकृतिबंध (vertex figure) संपूर्ण घनाकृतीची रचना ठरवून टाकतो असे युक्लिड व त्याच्या आधीचे ग्रीक गणिती मानून चालले. आपणही तसेच मानले, व म्हणून {3, 3}, {4, 3}, {3, 4}, {5, 3}, {3, 5} या पाच श्लेफ्ली चिह्नांपैकी प्रत्येक चिह्न असणारी एकेक घनाकृती मिळाल्यावर सुसम घनाकृती फक्त पाच असल्याचा निर्वाळा दिला. हे अनुमान अंततः योग्य निघाले, पण ते सिद्ध करण्याचे काम 1840च्या सुमारास ऑगस्तिन-लुइ कोशी (Augustin-Louis Cauchy) याने केले. त्यासाठी बहिर्वक्र बहुफलकांना लागू पडणारी दृढतेची संकल्पना (concept of rigidity) वापरावी लागते. असो.
सुसम बहुफलकाच्या फलकांची, कडांची व शिरोबिंदूंची संख्या
समजा एका सुसम बहुफलकाचे श्लेफ्ली चिह्न आहे {p, q}. मग त्याचा प्रत्येक फलक p बाजूंचा सुसम बहुभुज आहे आणि त्या बहुफलकाच्या प्रत्येक शिरोबिंदूपाशी q फलक येऊन मिळतात. अशा सुसम बहुभुजाच्या फलकांची (Faces) संख्या F असेल तर त्या फलकांच्या सगळ्या बाजूंची बेरीज होते pF, व तसेच त्यांच्या सगळ्या कोपऱ्यांचीही बेरीज होते pF. पण प्रत्येक बाजू 2 फलकांना सामाईक असल्यामुळे त्या सुसम बहुभुजाच्या एकूण कडांची (Edges) संख्या असली पाहिजे E = pF/2, व प्रत्येक कोपरा q फलकांना सामाईक असल्यामुळे त्या सुसम बहुभुजाच्या एकूण शिरोबिंदूंची (Vertices) संख्या असली पाहिजे V = pF/q. या हिशोबानुसार आपण शोधलेल्या सुसम बहुभुजांच्या फलकांची, कडांची आणि शिरोबिंदूंची गणना खाली दिलेल्या कोष्टकात केली आहे.
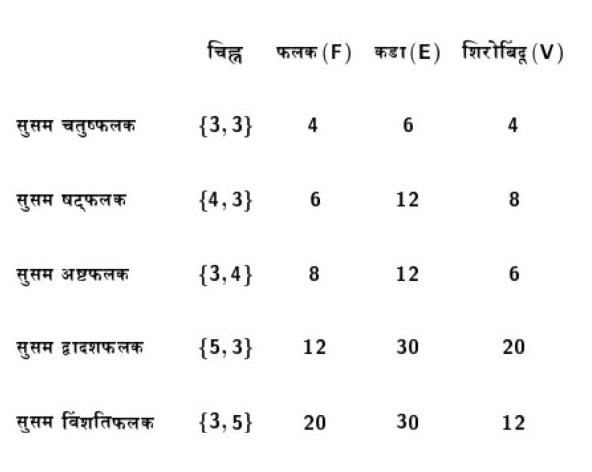
ह्या कोष्टकातील नोंदी न्याहाळून पाहिल्या की काही गोष्टी चटकन डोळ्यात भरतात त्या अशा – फक्त चतुष्फलकाच्या फलकांची संख्या आणि शिरोबिंदूंची संख्या समान आहे. षट्फलक आणि अष्टफलक यांबाबत फलकांच्या संख्येत आणि शिरोबिंदूंच्या संख्येत अदलाबदल झाली आहे, पण त्यांच्या कडांची संख्या समान आहे; तसेच झाले आहे द्वादशफलक आणि विंशतिफलक यांबाबत. हीच परिस्थिति या पाच सुसम बहुफलकांच्या श्लेफ्ली चिह्नांतील p, q या संख्यांबाबत दिसून येईल. काहीतरी पाणी नक्कीच मुरते आहे. फार खोलात न शिरता इतकेच सांगता येईल की प्रत्येक सुसम बहुफलकाशी संबंधित असा एक प्रतिरूप बहुफलक (dual polyhedron) असतो; एकाचे फलक दुसऱ्याच्या शिरोबिंदूंशी निगडित असतात आणि एकाच्या दोन शिरोबिंदू जोडणाऱ्या कडा दुसऱ्याच्या दोन फलकामधील सामाईक कडांशी निगडित असतात. खालील चित्रावरून सुसम षट्फलक (लाल) आणि सुसम अष्टफलक (पिवळा) एकमेकांचे प्रतिरूप कसे आहेत ते लगेच समजून येईल.

त्याचप्रमाणे सुसम द्वादशफलक आणि सुसम विंशतिफलक एकमेकांचे प्रतिरूप आहेत. सुसम चतुष्फलकाचा प्रतिरूप बहुफलक सुसम चतुष्फलकच आहे, म्हणजे तो स्वप्रतिरूप (self-dual) आहे. यांमुळेच वरील कोष्टकांतील काही नोंदींनी लक्ष वेधून घेतले.
लिओनार्ड ऑयलर (Leonhard Euler) या स्विस गणितज्ञाने 1758 साली कोणत्याही बहिर्वक्र बहुफलकाच्या शिरोबिंदूंची संख्या V, कडांची संख्या E आणि फलकांची संख्या F यांना जोडणारे एक अजब सूत्र शोधले: V – E + F = 2 असे. आपल्या पाचही सुसम बहुफलकांबाबत हे सूत्र सहज पडताळून पाहता येते; तसेच या सूत्रामध्ये आपण मिळवलेल्या V = pF/q आणि E = pF/2 या किंमती घातल्या तर आपल्याला {p, q} हे श्लेफ्ली चिह्न असलेल्या सुसम बहुभुजाच्या फलकांची संख्या मिळते F = 4q/(2p – pq + 2q) अशी. हे समीकरणही आपण पाच सुसम बहुफलकांबाबत सहज पडताळून पाहू शकतो. थोडक्यात, एकदा सुसम बहुभुजाचे श्लेफ्ली चिह्न {p, q} कळले की त्याच्या फलकांची, कडांची आणि शिरोबिंदूंची संख्या ठरून जाते.
समारोप
अखेरीस आपण चर्चा केलेल्या विषयाचा आढावा घेऊ या. मानवाला आदिकाळापासून सममित गोष्टींचे आकर्षण वाटत आले आहे. दोन मितींच्या प्रतलावर, म्हणजे कागदावर, पूर्णतः सममित अशा वेगवेगळ्या आकाराच्या अनंत चित्राकृती काढता येतात. खरोखर, p हा कोणताही दोनपेक्षा मोठा पूर्णांक असेल तर आपण p बाजू असलेला सुसम बहुभुज काढू शकतो, ज्याच्या सगळ्या बाजू समान लांबीच्या असतात व सगळे आंतरकोन समान असतात. मात्र तीन मितींच्या अवकाशात पूर्णतः सममित अशा फक्त पाचच घनाकृती बनवता येतात; त्यांना 4, 6, 8, 12 किंवा 20 फलक असतात. प्रत्येकीचे सगळे फलक एकाच आकाराचे सुसम बहुभुज असतात व तिच्या प्रत्येक शिरोबिंदूपाशी येऊन मिळणाऱ्या फलकांची संख्या समान असते. या घनाकृती खाली दाखवल्या आहेत.

प्लेटोच्या पाच घनाकृती
दोन मितींच्या प्रतलावर अनंत सुसम चित्राकृती पण तीन मितींच्या अवकाशात फक्त पाच सुसम घनाकृती असा विस्मयजनक फरक का असावा? या प्रश्नाचे उत्तर सोपे नाही. पण तुलनेसाठी असेच एक दुसरे गणिती प्रमेय सांगता येईल. x2 + y2 = z2 हे समीकरण साधणारे x, y, z असे धन पूर्णांक (positive integers) अनंत आहेत, जसे 3, 4, 5 किंवा 5, 12 , 13 किंवा 8, 15, 17 वगैरे. परंतु x, y, z यांचे वर्ग करण्याऐवजी घन करून मिळणारे x3 + y3 = z3 हे समीकरण साधणारे धन पूर्णांक असूच शकत नाहीत. हे विधान लिओनार्ड ऑयलरने 1770 साली सिद्ध केले. (दुवा) अशा गोष्टींची कारणमीमांसा देण्यासाठी सांगोपांग विश्लेषण (elaborate analysis) करावे लागते. पण अशी तर्कशुद्ध उत्तरे आपण देऊ शकतो ही गणिताची शक्ती आहे, गणितज्ञांची खरी कमाई आहे.
तीनपेक्षा अधिक मिती असलेल्या विश्वात आपल्याला किती पूर्णतः सममित आकृती मिळू शकतात याचा विचार आपण या लेखाच्या तिसऱ्या भागात करू. तेथेही काही अनपेक्षित गोष्टी आढळणार आहेत.
(खूपशा आकृती आंतरजालावरून साभार उसनवार)
(क्रमशः)
---
बालमोहन लिमये
(balmohan.limaye@gmail.com)

लेखकाचा अल्प-परिचय : मुंबईच्या आय्. आय्. टी.मधील गणित विभागात ४२ वर्षे काम केल्यानंतर आता गुणश्री प्राध्यापक (Professor Emeritus). पवईलाच रहिवास.
बालमोहन लिमये यांचे इतर लिखाण


प्रतिक्रिया
सूर्यमालेतले ग्रह आणि सुसम बहुफलक
सूर्यमालेतले ग्रह आणि सुसम बहुफलक ह्या कशाचं काही देणंघेणं नसलेल्या दोन विषयांतला परस्परसंबंध योहान केप्लरने ‘शोधून’ काढला होता हे मला पूर्वीपासून ठाऊक होतं. पण तपशील ठाऊक नव्हता. ह्या लेखाच्या निमित्ताने ह्या प्रकरणात डोकं घालण्याचं मी ठरवलं.
तर तो संबंध असा आहे:
(अ) बुध, शुक्र, पृथ्वी, मंगळ, गुरू आणि शनि हे पहिले सहा ग्रह घ्या. (केप्लरच्या वेळी इतकेच ठाऊक होते.) यांतला प्रत्येक ग्रह सूर्याभोवती वर्तुळाकार फिरतो. (अचूक वर्तुळात नव्हे, पण ते सध्या जाऊ दे.) यापैकी प्रत्येक वर्तुळाची त्रिज्या मोजा. कलेकलेने वाढत जाणारे असे सहा आकडे आपल्याला मिळतील.
(ब) आता सुसम बहुफलकांकडे वळू. उदाहरणार्थ, घन (म्हणजेच सुसम ६-फलक) डोळ्यांसमोर आणा. ह्या घनाच्या आत बरोब्बर बसणारा (आणि बाजूंना आतून स्पर्श करणारा) एक चेंडू असणार; त्याला ह्या घनाचा अंतर्गोल म्हणू. त्याचप्रमाणे घनाच्या सगळ्या शिरोबिंदूंतून जाणाराही एक चेंडू असणार; त्याला घनाचा बहिर्गोल म्हणू. बहिर्गोल हा अंतर्गोलापेक्षा मोठा असणार हे उघड आहे. त्याचप्रमाणे प्रत्येक सुसम बहुफलकाला एक अंतर्गोल आणि एक बहिर्गोल असतो.
इथपर्यंत सोपं आहे, पण पुढची पायरी थोडी किचकट आहे.
आपल्याला ठाऊक असलेले पाच बहुफलक एका निश्चित क्रमाने मांडायचे आहेत, आणि त्यांचा आकार एका विशिष्ट पद्धतीने ठरवायचा आहे.
(१) एक कुठल्याही आकाराचा ८-फलक घेऊन त्याच्या अंतर्गोलाची आणि बहिर्गोलाची त्रिज्या मोजा.
(२) आता हा बहिर्गोल ज्याचा अंतर्गोल असेल असा २०-फलक घ्या (आकार कितीही लहानमोठा करता येत असल्यामुळे हे सहज शक्य आहे), आणि त्या २०-फलकाच्या बहिर्गोलाची त्रिज्या मोजा.
हेच पुढे चालू ठेवा.
(३) हा बहिर्गोल ज्याचा अंतर्गोल असेल असा १२-फलक घेऊन त्याच्या बहिर्गोलाची त्रिज्या मोजा.
(४) हा बहिर्गोल ज्याचा अंतर्गोल असेल असा ४-फलक घेऊन त्याच्या बहिर्गोलाची त्रिज्या मोजा.
(५) हा बहिर्गोल ज्याचा अंतर्गोल असेल असा ६-फलक घेऊन त्याच्या बहिर्गोलाची त्रिज्या मोजा.
इतकं सगळं केल्यानंतर कलेकलेने वाढत जाणारे सहा आकडे आपल्याला मिळतील. पायरी (१) मध्ये दोन आकडे, आणि त्यानंतरच्या प्रत्येक पायरीत एकेक आकडा.
------
आता केप्लरचं निरीक्षण असं की (अ) मधल्या सहा आकड्यांची परस्परगुणोत्तरं आणि (ब) मधल्या सहा आकड्यांची परस्परगुणोत्तरं (अंदाजे) सारखीच आहेत. १५९६ साली ‘मिस्टीरीयुम कॉस्मोग्राफिकुम्’ ह्या ग्रंथात त्याने हे मांडलं.
ह्या ‘शोधा’बद्दल बरंच काही म्हणता येईल. एकतर तो पूर्णपणे बोगस आहे. म्हणजे ह्या दोन विषयांचा एकमेकांशी खरोखर काही संबंध नाही, आणि आकडे कसेबसे जुळून येतात हा निव्वळ योगायोग आहे. (आणि म्हणूनच मी प्रत्यक्ष आकडे इथे दिलेले नाहीत.)
पण केप्लरच्या चिकाटीचं कौतुक वाटतं. एवढ्या सगळ्या गोलांच्या त्रिज्या गणिताने काढणं हे काम इतकं किचकट आहे की प्रचंड प्रमाणात श्रमांची, कागदाची, शाईची आणि कंदिलाच्या तेलाची नासाडी केल्याखेरीज ते शक्य नाही. पण असले प्रकार केप्लरच्या हाडात मुरलेले होते. पराकोटीचा कष्टाळू आणि एककल्ली असा तो इसम होता.
ज्याला खगोलशास्त्रातला केप्लरचा दुसरा आणि तिसरा नियम म्हणतात तेही असेच पानंच्या पानं किचकट आकडेमोडी करून त्याने शोधून काढलेले आहेत. फरक इतकाच की हे नियम मात्र ‘खरे’ आहेत: म्हणजे न्यूटनचा गुरुत्वाकर्षणाचा सिद्धान्त वापरून ते शाबीत करता येतात.
बहुमोलाचा शास्त्रीय शोध कष्टसाध्य असतो आणि कचराही कष्टसाध्य असतो.
-------
- जयदीप चिपलकट्टी
(होमपेज)
छान
छान पुरवणी आहे ही.
Along the same lines
Along the same lines (planetary distances from Sun) is this interesting empirical observation ("law"?) is the Titius-Bode law. Not sure if Kepler's numbers and Bode's llaw has any connection. Although this "law' has been proven to not work for Neptune, it is an interesting observation.
https://en.wikipedia.org/wiki/Titius%E2%80%93Bode_law#:~:text=The%20Titi...(sometimes,Sun%20as%20the%20one%20before.
पुरवणी
वरची पुरवणी छान आहेच पण प्रश्न असा उभा राहतो की हा उद्योग करावा असे केप्लरला का वाटले असावे? तसेच वर दिलेल्या पायऱ्यांपैकी (३), (४) आणि (५) ह्या पायऱ्यांमधील १२, ४ आणि ६ ह्या संख्या त्याने का निवडल्या असाव्यात?
असाच out of context एक अजूनहि विषय मला दिसतो आणि तो येथे नोंदविण्याचा मोह आवरत नाही. सूर्यमालेतले ग्रह आणि आठवड्याच्या दिवसांची नावे ह्या परस्परांशी उघड संबंध नसलेल्या गोष्टींमधील संबंध येथे नमूद करावासा वाटतो.
मराठीत ’होरा’ म्हणजे भविष्याची कल्पना किंवा तर्क, ज्यावरून ज्योतिषांना आदरपूर्वक ’होराभूषण’ असे संबोधले जाते. मूळचा खाल्डियन भाषेतील ’दिवसाचा २४ वा भाग अशा अर्थाचा हा शब्द ग्रीक भाषेमध्ये ώρα असा बदलून तेथून भारतीय ज्योतिषात त्याच अर्थाने प्रचलित झाला. (इंग्रजी hour हा शब्दहि त्याच उगमाचा.) भारतीय ज्योतिषात दिवसाच्या २४ तासांना क्रमाने एकेक ग्रह ’होरेश’ मानला जातो आणि त्यांचा क्रम पृथ्वीभोवतीच्या त्यांच्या प्रदक्षिणाकालाच्या उतरत्या क्रमाने शनि, गुरु, मंगळ, रवि, शुक्र, बुध आणि चंद्र (सोम) असा असतो. आजच्या दिवसाचा पहिला होरेश शनि असला तर आजचा वार शनिवार. उतरत्या क्रमाने तीन आवर्तनांनंतर आजचा शेवटचा होरेश मंगळ आणि उद्याचा पहिला होरेश रवि म्हणून उद्याचा दिवस रविवार आणि ह्याच क्रमाने सोमवार, मंगळवार इत्यादि निर्माण होतात. ’होरा’ शब्दाच्या मूळ अर्थाची विस्मृति होऊन त्याला ’भविष्य’ हा अर्थ चिकटला.
.
> वरची पुरवणी छान आहेच पण प्रश्न असा उभा राहतो की हा उद्योग करावा असे केप्लरला का वाटले असावे? तसेच वर दिलेल्या पायऱ्यांपैकी (३), (४) आणि (५) ह्या पायऱ्यांमधील १२, ४ आणि ६ ह्या संख्या त्याने का निवडल्या असाव्यात?
---
माझा तर्क असा की हा केप्लरच्या मनोवृत्तीचा भाग होता. विश्वाच्या रचनेत संपूर्ण सुसूत्रता आहे (म्हणजे भौतिक जग, गणिती जग, मानवी शरीराची आणि मनाची रचना ह्या सगळ्यांतच इकडून तिकडे जाणारे अदृश्य धागे आहेत) असं एकदा डोक्यात घेतलं की असे भास होणं साहजिक आहे. आकाशात सहा ग्रह आहेत आणि गणितात पाच बहुफलक आहेत हा योगायोग नसणार असं एकदा ठरवलं आणि खूप कष्ट घ्यायची तयारी असली की काहीतरी संबंध केव्हातरी सापडेलच. समजा ४, १२, ६ हा क्रम नीट ‘बसला’ नाही, तर १२,४,६ बसतो का हे बघता येईल. तो ही बसला नसता तर पुन्हा बदलून बघता आला असता. बहिर्गोलाची त्रिज्या नीट बसली नाही तर त्रिज्येचा वर्ग बसतो का हे पाहता आलं असतं.
अशाचप्रकारे त्याने ‘हार्मोनिका मुंडी’ (म्हणजे विश्वसंगीत) ह्या ग्रंथात संगीतातल्या सुरांच्या कंप्रता (डो-रे-मि-फा इत्यादि) आणि बहुफलक यांचा संबंध जोडण्याचा प्रयत्न केला आहे. ते सुद्धा निरर्थक संशोधनच मानावं लागेल.
केप्लर हा खगोलशास्त्रज्ञ म्हणून प्रसिद्ध आहे (आणि ते योग्यच आहे) पण त्याला ज्योतिषातही (म्हणजे ग्रहताऱ्यांचा अभ्यास करून भविष्य सांगण्यात) खूप रस होता. त्याही खटाटोपात त्याने असेच अतोनात निष्फळ कष्ट घेतलेले आहेत. युरोपातल्या thirty years war (१६१८-४८) चा काही भाग त्याच्या हयातीत होऊन गेला. त्या काळी ग्रहांकडे बघून कसलंही आणि कितीही वाईट भाकीत वर्तवलं तरी युरोपात कुठे ना कुठे ते खरं ठरतंच असे.
----
‘होरा’ ह्या शब्दाची व्युत्पत्ती अतिशय रंजक आहे. होरारत्न, होराभूषण हे शब्द लहानपणापासून ऐकत आलो आहे, पण hour-horloge-horoscope शी त्याचा संबंध असेल अशी शंका देखील आली नव्हती.
- जयदीप चिपलकट्टी
(होमपेज)